题目内容
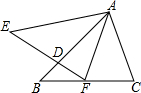 (2013•永安市质检)如图,△ABC绕点A旋转至△AEF,使点C的对应点F落在BC上,给出下列结论:
(2013•永安市质检)如图,△ABC绕点A旋转至△AEF,使点C的对应点F落在BC上,给出下列结论:①∠AFC=∠C ②DE=CF
③△ADE∽△FDB ④∠BFD=∠CAF
其中正确的结论是
①③④
①③④
(写出所有正确结论的序号).分析:根据旋转的性质可得AF=AC,再根据等边对等角可得∠AFC=∠C,判断出①正确;AE>AD,从而求出∠E≠∠ADE,即∠B≠∠BDF,得到BF≠DF,然后根据DE=EF-DF,CF=BC-BF得到DE≠CF,判断出②错误;根据两组角对应相等两三角形相似可得△ADE和△FDB相似,判断出③正确;根据平角定义表示出∠BFD,根据三角形内角和定理表示出∠CAF,从而得到∠BFD=∠CAF,判断出④正确.
解答:解:由旋转的性质得,AF=AC,
∴∠AFC=∠C,故①正确;
∵AE=AB>AD,
∴∠E≠∠ADE,
即∠B≠∠BDF,
∴BF≠DF,
∵DE=EF-DF,CF=BC-BF,EF=BC,
∴DE≠CF,故②错误;
∵△ABC绕点A旋转至△AEF,
∴∠B=∠E,
又∵∠ADE=∠BDF,
∴△ADE∽△FDB,故③正确;
由旋转的性质,∠C=∠AFE,
∴∠BFD=180°-∠AFC-∠AFE=180°-2∠C,
在△ACF中,∠CAF=180°-∠AFC-∠C=180°-2∠C,
∴∠BFD=∠CAF,故④正确;
综上所述,正确的结论有①③④.
故答案为:①③④.
∴∠AFC=∠C,故①正确;
∵AE=AB>AD,
∴∠E≠∠ADE,
即∠B≠∠BDF,
∴BF≠DF,
∵DE=EF-DF,CF=BC-BF,EF=BC,
∴DE≠CF,故②错误;
∵△ABC绕点A旋转至△AEF,
∴∠B=∠E,
又∵∠ADE=∠BDF,
∴△ADE∽△FDB,故③正确;
由旋转的性质,∠C=∠AFE,
∴∠BFD=180°-∠AFC-∠AFE=180°-2∠C,
在△ACF中,∠CAF=180°-∠AFC-∠C=180°-2∠C,
∴∠BFD=∠CAF,故④正确;
综上所述,正确的结论有①③④.
故答案为:①③④.
点评:本题考查了旋转的性质,等边对等角的性质,相似三角形的判定,三角形的内角和定理,熟记各性质并准确识图,理清角度之间的关系是解题的关键.

练习册系列答案
相关题目
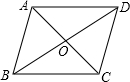 (2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是
(2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是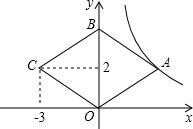 (2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数
(2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数