题目内容
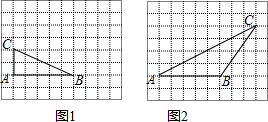
(2013•道外区一模)图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,请在图1、图2中各取一点C(点C必须在小正方形的顶点上),使以A、B、C为顶点的三角形分别满足以下要求:
(1)在图1中画一个△ABC,使△ABC为面积为5的直角三角形;
(2)在图2中画一个△ABC,使△ABC为钝角等腰三角形.

(1)在图1中画一个△ABC,使△ABC为面积为5的直角三角形;
(2)在图2中画一个△ABC,使△ABC为钝角等腰三角形.

分析:(1)根据题意可知AB=5,要使△ABC面积为5,则只需要过点A作垂直AB的直线且长度为2即可;
(2)要使△ABC为钝角等腰三角形,则必须找到和AB相等的边BC且C点必须在小正方形的顶点.
(2)要使△ABC为钝角等腰三角形,则必须找到和AB相等的边BC且C点必须在小正方形的顶点.
解答:解:(1)∵AB=5,
∴要使△ABC面积为5,则只需要过点A作垂直AB的直线且长度为2即可,
如图所示;
(2)BC=
=5=AB,
如图所示.
 (答案不唯一)
(答案不唯一)
∴要使△ABC面积为5,则只需要过点A作垂直AB的直线且长度为2即可,
如图所示;
(2)BC=
| 32+42 |
如图所示.
 (答案不唯一)
(答案不唯一)点评:本题考查了勾股定理的应用及三角形面积的知识,难度一般,有多种画法,只需满足题目条件即可.

练习册系列答案
相关题目
 (2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )
(2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )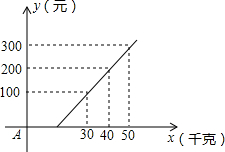 (2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )
(2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )