题目内容
 (2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )
(2013•道外区一模)如图,在△ABC中,AB=AC,∠ABC=40°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接BD,则∠DBC的度数为( )分析:根据旋转的性质得∠BAD=20°,AB=AD,根据等腰三角形的性质得∠ABD=∠ADB,则∠ABD=
(180°-20°)=80°,然后利用∠DBC=∠ABD-∠ABC计算即可.
| 1 |
| 2 |
解答:解:∵△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),
∴∠BAD=20°,AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=
(180°-20°)=80°,
∵∠ABC=40°,
∴∠DBC=80°-40°=40°.
故选D.
∴∠BAD=20°,AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=
| 1 |
| 2 |
∵∠ABC=40°,
∴∠DBC=80°-40°=40°.
故选D.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰三角形的性质.

练习册系列答案
相关题目
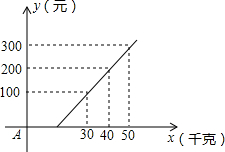 (2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )
(2013•道外区一模)如图所示,是某航空公司托运行李的费用y(元)与行李重量x(千克)的关系图象,由图中可知,乘客可以免费托运行李的最大重量为( )