Question

反比例函数y=

k

x

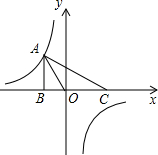
在第四象限的双曲线上有一点A，AB⊥x轴于B，OA=10，OB：AB=3：4
（1）求反比例函数的解析式；
（2）将OB沿OC对折，使它落在斜边OA上与OD重合，求C点坐标？
（3）在x轴上是否存在点P使△POC为等腰三角形？不存在，说明理由；若存在，直接写出P的坐标（3个即可）

Answer 1

（1）∵Rt△OAB中，OA=10，OB：AB=3：4，
∴设OB=3x，AB=4x，
∴（3x）²+（4x）²=10²，解得x=2，
∴OB=6，AB=8，即A（6，-8），B（6，0），
∵点A在反比例函数y=

k

x

的图象上，
∴k=6×（-8）=-48，
∴反比例函数的解析式为：y=-

48

x

；

（2）∵△ODC由△OBC反折而成，
∴OD=OB=6，BC=DC，
∵OA=10，
∴AD=OA-OD=10-6=4，
设BC=a，则AC=8-a，
在Rt△ACD中，AD²+CD²=AC²，即4²+a²=（8-a）²，解得a=3，
∴C（6，-3）；

（3）设P（p，0），
∵C（6，-3），
∴OC=

62+(-3)2

=3

5

，
当OP=OC时，OP=3

5

，
∴P₁（3

5

，0），P₂（-3

5

，0）；
当OP=PC时，p²=（p-6）²+（-3）²，解得p=

15

4

，
∴P₃（

15

4

，0）；
当OC=PC时，（p-6）²+3²=（3

5

）²，解得p=12或p=0（舍去），
∴P₄（12，0）．
综上所述，P₁（3

5

，0），P₂（-3

5

，0），P₃（

15

4

，0），P₄（12，0）．