题目内容
如图,等腰梯形ABCD中,AD∥BC,AB=CD,AD=10 cm,BC=30 cm,动点P从点A开始沿AD边向点D以每秒1厘米的速度运动,同时点Q从点C开始沿CB边向点B以每秒3厘米的速度运动,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.
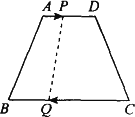
(1)t为何值时,四边形ABQP为平行四边形?
(2)四边形ABQP能成为等腰梯形吗?如果能,求出t的值;如果不能,请说明理由.
答案:
解析:
提示:
解析:
|
思路与技巧:动点问题关键抓住如何运动,如其方向、速度及其轨迹.要使其为 |
提示:
|
转化是数学中一种思想方法,学会转化,如(2)中的要使ABQP四边形为等腰梯形,即四边形PQCD为平行四边形,问题就极易解决. |

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.