题目内容
 18、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为5.4米,则树高为
18、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为5.4米,则树高为14.3
米.分析:在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,据此可构造出相似三角形.
解答: 解:根据题意可构造相似三角形模型如图:
解:根据题意可构造相似三角形模型如图:
则其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地上部分的长,ED的长为台阶高,并且由光沿直线传播的性质可知BC即为树影在地上的全长,
延长FE交AB于G,则Rt△ABC∽Rt△AGF,
∴AG:GF=AB:BC=物高:影长=1:0.4,
∴GF=0.4AG,
又∵GF=GE+EF,BD=GE,
∴GF=5.6,
∴AG=14,
∴AB=AG+GB=14.3,
即树高为14.3米,
故答案为14.3.
 解:根据题意可构造相似三角形模型如图:
解:根据题意可构造相似三角形模型如图:则其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地上部分的长,ED的长为台阶高,并且由光沿直线传播的性质可知BC即为树影在地上的全长,
延长FE交AB于G,则Rt△ABC∽Rt△AGF,
∴AG:GF=AB:BC=物高:影长=1:0.4,
∴GF=0.4AG,
又∵GF=GE+EF,BD=GE,
∴GF=5.6,
∴AG=14,
∴AB=AG+GB=14.3,
即树高为14.3米,
故答案为14.3.
点评:本题考查了直角三角形的有关知识,同时渗透光学中光的传播原理,构造直角形是解决本题关键,属于中等题目.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
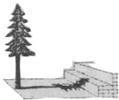 兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( )
兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( ) 6、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为l米的竹竿的影长为0.5米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( )
6、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为l米的竹竿的影长为0.5米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为( ) 24、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米.
24、兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米. (2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米?
(2013•响水县一模)兴趣小组的同学要测量教学楼前一棵树的高度.在阳光下,一名同学测得一根竖直在地面上的长为1米的竹竿的在地面上的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此台阶上影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则此树高为多少米?