题目内容
有理数a,b,c均不为0,且a+b+c=0,设x=| |a| |
| b+c |
| |b| |
| c+a |
| |c| |
| a+b |
分析:由a+b+c=0可得a=-(b+c),b=-(a+c),c=-(a+b),且必有一个大于0,一个小于0,可令a>0,c<0,据此可得出x的值.
解答:解:有理数a,b,c均不为0可得a、b、c必有一个大于0,一个小于0,可令a>0,c<0,
∴x=-1+
+1=±1.
故填±1.
∴x=-1+
| |b| |
| -b |
故填±1.
点评:本题考查绝对值的知识,有一定的难度,得出a、b、c必有一个大于0,一个小于0的结论是本题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
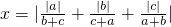 ,试求代数式x19+99x+2000之值.
,试求代数式x19+99x+2000之值.