题目内容
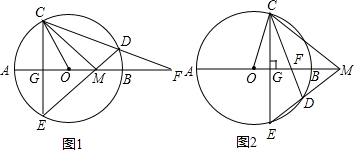
如图1,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在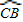 上取一点D,分别作直线PA、ED,交直线AB于点F、M.
上取一点D,分别作直线PA、ED,交直线AB于点F、M.(1)求∠COA和∠FDM的度数;
(2)求证:△FDM∽△COM;
(3)如图2,若将垂足G改取为半径OB上任意一点,点D改取在
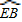 上,仍作直线PA、ED,分别交直线AB于点F、M.试判断:此时是否仍有△FDM∽△COM?证明你的结论.
上,仍作直线PA、ED,分别交直线AB于点F、M.试判断:此时是否仍有△FDM∽△COM?证明你的结论.
【答案】分析:(1)由于CG⊥OA,根据垂径定理可得出,弧CA=弧AE,那么根据圆周角定理可得出∠CDE=∠COA,在Rt△COG中,可根据OG是半径的一半得出∠AOC是60°,那么就能得出∠FDM=180°-∠CDE=120°
(2)在(1)中我们根据垂径定理得出OA是CE的垂直平分线,那么△CMG和△EMG全等,可得出∠CMA=∠EMG,也就可得出∠CMO=∠FMD,在(1)中已经证得∠AOC=∠EDC=60°,那么∠COM=∠MDF,因此两三角形就相似.
(3)可按(2)的方法得出∠DMF=∠CMO,关键是再找出一组对应角相等,还是用垂径定理来求,根据垂径定理我们可得出弧AC=弧AE,那么∠AOC=∠EDC,根据等角的余角相等即可得出∠COM=∠FDM,由此可证出两三角形相似.
解答:(1)解:∵AB为直径,CE⊥AB
∴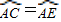 ,CG=EG
,CG=EG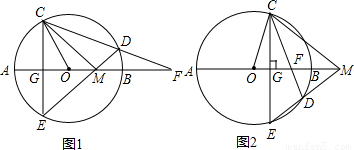
在Rt△COG中,
∵OC=OA,OG= OA,
OA,
∵OG= OC,
OC,
∴∠OCG=30°,
∴∠COA=60°,
又∵∠CDE的度数=
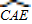 的度数=
的度数= 的度数=∠COA的度数=60°
的度数=∠COA的度数=60°
∴∠FDM=180°-∠CDE=120°.
(2)证明:∵∠COM=180°-∠COA=120°,
∴∠COM=∠FDM
在Rt△CGM和Rt△EGM中,
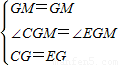
∴Rt△CGM≌Rt△EGM(SAS)
∴∠GMC=∠GME
又∵∠DMF=∠GME,
∴△FDM∽△COM.
(3)解:结论仍成立.
∵∠EDC的度数=
 的度数=
的度数=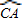 的度数=∠COA的度数,
的度数=∠COA的度数,
∴∠FDM=180°-∠COA=∠COM
∵AB为直径,
∴CE⊥AB,
在Rt△CGM和Rt△EGM中,
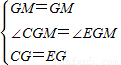
∴Rt△CGM≌Rt△EGM(SAS)
∴∠GMC=∠GME
∴△FDM∽△COM.
点评:本题主要考查了圆周角定理,垂径定理,全等三角形和相似三角形的判定及性质等知识点,根据垂径定理得出角相等是解题的关键.
(2)在(1)中我们根据垂径定理得出OA是CE的垂直平分线,那么△CMG和△EMG全等,可得出∠CMA=∠EMG,也就可得出∠CMO=∠FMD,在(1)中已经证得∠AOC=∠EDC=60°,那么∠COM=∠MDF,因此两三角形就相似.
(3)可按(2)的方法得出∠DMF=∠CMO,关键是再找出一组对应角相等,还是用垂径定理来求,根据垂径定理我们可得出弧AC=弧AE,那么∠AOC=∠EDC,根据等角的余角相等即可得出∠COM=∠FDM,由此可证出两三角形相似.
解答:(1)解:∵AB为直径,CE⊥AB
∴
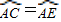 ,CG=EG
,CG=EG
在Rt△COG中,
∵OC=OA,OG=
 OA,
OA,∵OG=
 OC,
OC,∴∠OCG=30°,
∴∠COA=60°,
又∵∠CDE的度数=

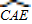 的度数=
的度数= 的度数=∠COA的度数=60°
的度数=∠COA的度数=60°∴∠FDM=180°-∠CDE=120°.
(2)证明:∵∠COM=180°-∠COA=120°,
∴∠COM=∠FDM
在Rt△CGM和Rt△EGM中,
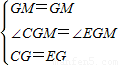
∴Rt△CGM≌Rt△EGM(SAS)
∴∠GMC=∠GME
又∵∠DMF=∠GME,
∴△FDM∽△COM.
(3)解:结论仍成立.
∵∠EDC的度数=

 的度数=
的度数=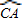 的度数=∠COA的度数,
的度数=∠COA的度数,∴∠FDM=180°-∠COA=∠COM
∵AB为直径,
∴CE⊥AB,
在Rt△CGM和Rt△EGM中,
∴Rt△CGM≌Rt△EGM(SAS)
∴∠GMC=∠GME
∴△FDM∽△COM.
点评:本题主要考查了圆周角定理,垂径定理,全等三角形和相似三角形的判定及性质等知识点,根据垂径定理得出角相等是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

 M.试判断:此时是否仍有△FDM∽△COM?证明你的结论.
M.试判断:此时是否仍有△FDM∽△COM?证明你的结论.
 如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点.
如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径为AB,P为AB上一点,点C、D为半圆O的三等分点,若阴影部分的面积为6πcm2,则半圆O的半径为
如图,半圆O的直径为AB,P为AB上一点,点C、D为半圆O的三等分点,若阴影部分的面积为6πcm2,则半圆O的半径为