题目内容
已知AB与⊙O相切于点C,OA=OB,OA、OB与⊙O分别交于点D、E.(I)如图①,若⊙O的直径为8,AB=10,求OA的长(结果保留根号);
(II)如图②,连接CD、CE,若四边形ODCE为菱形,求
| OD | OA |

分析:(1)连接OC,根据切线的性质得出OC⊥AB,再由勾股定理求得OA即可;
(2)根据菱形的性质,求得OD=CD,则△ODC为等边三角形,可得出∠A=30°,即可求得
的值.
(2)根据菱形的性质,求得OD=CD,则△ODC为等边三角形,可得出∠A=30°,即可求得
| OD |
| OA |
解答: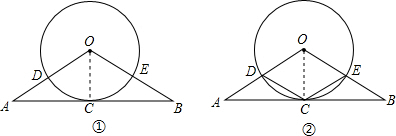 解:(1)如图①,连接OC,则OC=4,
解:(1)如图①,连接OC,则OC=4,
∵AB与⊙O相切于点C,∴OC⊥AB,
∴在△OAB中,由AO=OB,AB=10,
得AC=
AB=5.
在Rt△AOC中,由勾股定理得OA=
=
=
;
(2)如图②,连接OC,则OC=OD,
∵四边形ODCE为菱形,∴OD=CD,
∴△ODC为等边三角形,有∠AOC=60°.
由(1)知,∠OCA=90°,∴∠A=30°,
∴OC=
OA,∴
=
.
 解:(1)如图①,连接OC,则OC=4,
解:(1)如图①,连接OC,则OC=4,∵AB与⊙O相切于点C,∴OC⊥AB,
∴在△OAB中,由AO=OB,AB=10,
得AC=
| 1 |
| 2 |
在Rt△AOC中,由勾股定理得OA=
| OC2+AC2 |
| 42+52 |
| 41 |
(2)如图②,连接OC,则OC=OD,
∵四边形ODCE为菱形,∴OD=CD,
∴△ODC为等边三角形,有∠AOC=60°.
由(1)知,∠OCA=90°,∴∠A=30°,
∴OC=
| 1 |
| 2 |
| OD |
| OA |
| 1 |
| 2 |
点评:本题考查了切线的性质和勾股定理以及直角三角形、菱形的性质,是一道综合题,要熟练掌握.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 的值.
的值.
 的值。
的值。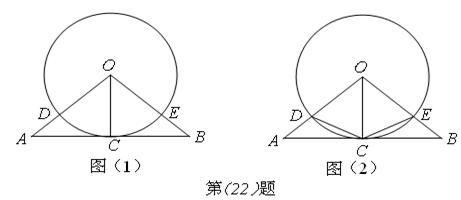
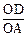 的值。
的值。