题目内容
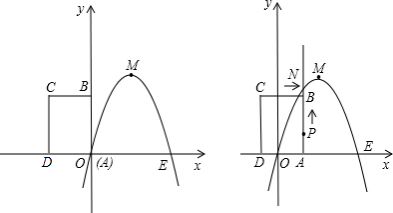
如图，已知抛物线经过
，
两点，顶点为
．
（1）求抛物线的解析式；
（2）将绕点
顺时针旋转90°后，点
落到点
的位置，将抛物线沿
轴平移后经过点
，求平移后所得图象的函数关系式；
（3）设（2）中平移后，所得抛物线与轴的交点为
，顶点为
，若点
在平移后的抛物线上，且满足
的面积是
面积的2倍，求点
的坐标．
略
解析:解:（1）已知抛物线经过
，
解得
所求抛物线的解析式为
． 3分
（2），
，
可得旋转后点的坐标为
4分
当时，由
得
，
（3）可知抛物线过点
将原抛物线沿
轴向下平移1个单位后过点
．
平移后的抛物线解析式为：
． 5分
练习册系列答案
相关题目
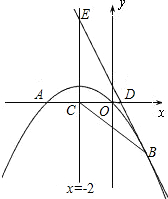2x+1经过抛物线上一点B（2，m），且与y轴．直线x=-2分别交于点D、E．
（2013•衡阳）如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=-1．
如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B（-2，m），且与y轴、直线x=2分别交于点D、E，
如图，已知抛物线经过坐标原点，与x轴的另一个交点为A，且顶点M坐标为（1，2），