题目内容
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到
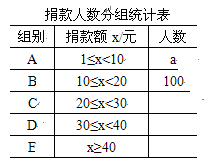
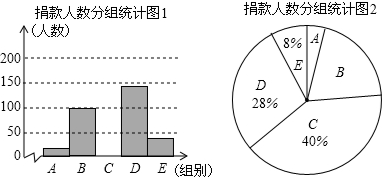
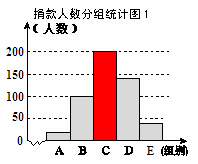
一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计(图
中信息不完整). 已知A、B两组捐款人数的比为1 : 5.
请结合以上信息解答下列问题.
(1) a= ,本次调查样本的容量是 ;
(2) 先求出C组的人数,再补全“捐款人数分组统计图1”;
(3) 若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?
一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计(图
中信息不完整). 已知A、B两组捐款人数的比为1 : 5.


请结合以上信息解答下列问题.
(1) a= ,本次调查样本的容量是 ;
(2) 先求出C组的人数,再补全“捐款人数分组统计图1”;
(3) 若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?
(1)20,500。(2)200,统计图见解析(3)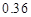
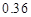
解:(1)20,500。
(2)∵500×40%=200,∴C组的人数为200。
补全“捐款人数分组统计图1”如图:
(3)∵D、E两组的人数和为:500×(28%+8%)=180,
∴捐款数不少于30元的概率是: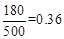 。
。
(1)根据A、B两组捐款的人数的比列式求解即可得到a的值,求出A、B两组捐款人数所占的百分比的和与A、B两组捐款的人数的和,列式计算即可求出样本容量:
∵A、B两组捐款人数的比为1:5,B组捐款人数为100人,
∴A组捐款人数为:100÷5=20。
∵A、B两组捐款人数所占的百分比的和为:1-40%-28%-8%=1-76%=24%,
A、B两组捐款的人数的和为:20+100=120,
∴本次调查样本的容量是120÷24%=500。
(2)用样本容量乘以C组人数所占的百分比,计算即可得解,然后再补全统计图。
(3)先求出D、E两组的人数的和,再根据概率公式列式计算即可,或直接求出D、E两组捐款人数所占的百分比的和即可。
(2)∵500×40%=200,∴C组的人数为200。
补全“捐款人数分组统计图1”如图:

(3)∵D、E两组的人数和为:500×(28%+8%)=180,
∴捐款数不少于30元的概率是:
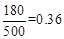 。
。(1)根据A、B两组捐款的人数的比列式求解即可得到a的值,求出A、B两组捐款人数所占的百分比的和与A、B两组捐款的人数的和,列式计算即可求出样本容量:
∵A、B两组捐款人数的比为1:5,B组捐款人数为100人,
∴A组捐款人数为:100÷5=20。
∵A、B两组捐款人数所占的百分比的和为:1-40%-28%-8%=1-76%=24%,
A、B两组捐款的人数的和为:20+100=120,
∴本次调查样本的容量是120÷24%=500。
(2)用样本容量乘以C组人数所占的百分比,计算即可得解,然后再补全统计图。
(3)先求出D、E两组的人数的和,再根据概率公式列式计算即可,或直接求出D、E两组捐款人数所占的百分比的和即可。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

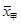 =80,
=80,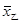 =90,方差分别是
=90,方差分别是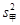 =10,
=10,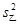 =5,比较这两组数据,下列说法正确的是( )。
=5,比较这两组数据,下列说法正确的是( )。
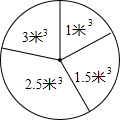
 ,7的平均数6,则
,7的平均数6,则 、
、 、
、 的值;并补全频数分布直方图;
的值;并补全频数分布直方图;