��Ŀ����
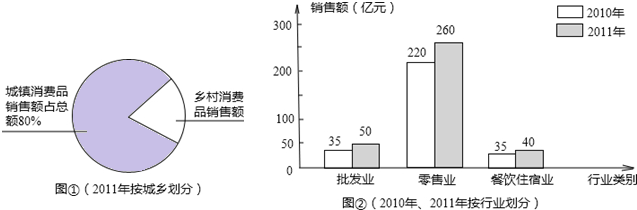
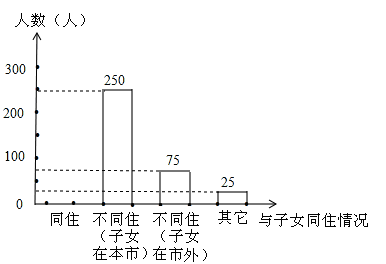
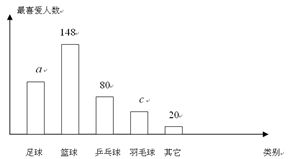
�����ԡ�Ȫˮ����������Ϊ����Ȫˮ���츣�������������л�����չ����ˮ��Ȫ������������ÿ���ʱ���ijС��300���������ˮ���������ͳ�ƣ�����5�·ݸ����������ˮ����4�·������½���������5�·ݸ�������Ľ�ˮ��ͳ����������ͳ��ͼ����
��1��300������5�·ݽ�ˮ������������λ���ֱ��Ƕ�����3��
��2������ͳ��ͼ��2.5��3��Ӧ���ε�Բ�Ľ�Ϊ �ȣ�
��3����С��300������5�·�ƽ��ÿ����Լ��ˮ������3��

| ��ˮ������3�� | 1 | 1.5 | 2.5 | 3 |
| �� �� | 50 | 80 | 100 | 700 |
��1��300������5�·ݽ�ˮ������������λ���ֱ��Ƕ�����3��
��2������ͳ��ͼ��2.5��3��Ӧ���ε�Բ�Ľ�Ϊ �ȣ�
��3����С��300������5�·�ƽ��ÿ����Լ��ˮ������3��
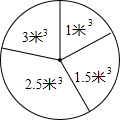
��1��2.5��3��2.5��3��2��120��3��2.1��3
�⣺��1������2.5������100�Σ�������࣬���Խ�ˮ����������2.5��3��
λ�ô����м�����ǵ�150���͵�151��������2.5������λ����2.5��3��
��2��120��
��3���ߣ�50��1+80��1.5+2.5��100+3��70����300=2.1����3����
���С��300������5�·�ƽ��ÿ����Լ��ˮ2.1��3��
��1��������һ�������г��ִ����������ݣ���һ�����ݰ��մ�С����Ӵ�С����˳����
�У�������ݵĸ����������������м�λ�õ��������������ݵ���λ�������ݶ������⡣
��2�����ȼ������ˮ��2.5��3��Ӧ�ľ���������ռ�ٷֱȣ�����360����ٷֱȼ��ɣ�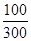 ��100%��360��=120�㡣
��100%��360��=120�㡣
��3�����ݼ�Ȩƽ������ʽ����n����x1��x2��x3������xn��Ȩ�ֱ���w1��w2��w3������wn����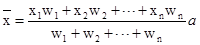 �����м��㼴�ɡ�
�����м��㼴�ɡ�
λ�ô����м�����ǵ�150���͵�151��������2.5������λ����2.5��3��
��2��120��
��3���ߣ�50��1+80��1.5+2.5��100+3��70����300=2.1����3����
���С��300������5�·�ƽ��ÿ����Լ��ˮ2.1��3��
��1��������һ�������г��ִ����������ݣ���һ�����ݰ��մ�С����Ӵ�С����˳����
�У�������ݵĸ����������������м�λ�õ��������������ݵ���λ�������ݶ������⡣
��2�����ȼ������ˮ��2.5��3��Ӧ�ľ���������ռ�ٷֱȣ�����360����ٷֱȼ��ɣ�
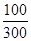 ��100%��360��=120�㡣
��100%��360��=120�㡣��3�����ݼ�Ȩƽ������ʽ����n����x1��x2��x3������xn��Ȩ�ֱ���w1��w2��w3������wn����
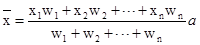 �����м��㼴�ɡ�
�����м��㼴�ɡ�
��ϰ��ϵ�д�
�����Ŀ
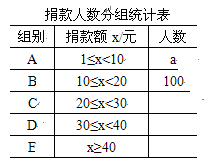
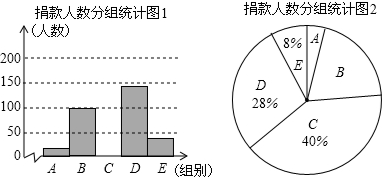

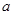
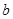
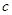
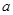 ����ȫ��ͬ��С��������5�������ñ�ǣ�Ȼ��Żش����н�����ȣ���������һ��������Ƿ��б���ٷŻش����н�����ȣ�ͨ�������ظ�ģ��������֣������б�ǵ����Ƶ���ȶ���20������ô���������
����ȫ��ͬ��С��������5�������ñ�ǣ�Ȼ��Żش����н�����ȣ���������һ��������Ƿ��б���ٷŻش����н�����ȣ�ͨ�������ظ�ģ��������֣������б�ǵ����Ƶ���ȶ���20������ô���������