题目内容
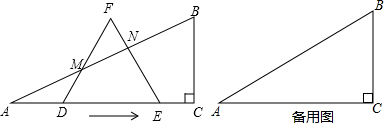
(2013•惠安县质检)把两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:
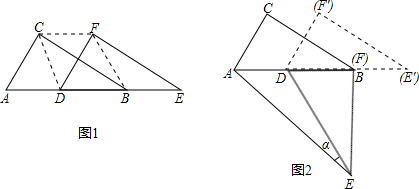
(1)如图1,将△DEF沿线段AB向右平移(即D点在线段AB内移动),当D点移至AB的中点时,连接DC、CF、FB,四边形CDBF的形状是
(2)如图2,将△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,则sinα的值等于
.

(1)如图1,将△DEF沿线段AB向右平移(即D点在线段AB内移动),当D点移至AB的中点时,连接DC、CF、FB,四边形CDBF的形状是
菱形
菱形
;(2)如图2,将△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连接AE,则sinα的值等于
| ||
| 14 |
| ||
| 14 |
分析:(1)根据直角三角形斜边上的中线等于斜边的一半和平移的性质,即可得到该四边形的四条边都相等,则它是一个菱形;
(2)过D点作DH⊥AE于H,可以把要求的角构造到直角三角形中,根据三角形ADE的面积的不同计算方法,可以求得DH的长,进而求解.
(2)过D点作DH⊥AE于H,可以把要求的角构造到直角三角形中,根据三角形ADE的面积的不同计算方法,可以求得DH的长,进而求解.
解答: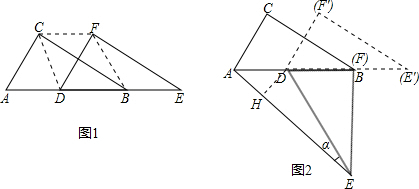 解:(1)如图1,∵D点是AB的中点,
解:(1)如图1,∵D点是AB的中点,
∴在直角三角形ABC中,
∴CD=AD=BD,
根据平移的性质得到CF=BD,BF=CD,
∴CF=BD=BF=CD,
∴四边形CDBF是菱形;
(2)如图2,在Rt△ABC中,
∵∠A=60°,AC=1,
∴BC=AC•tan60°=
,AB=
=2.
根据旋转的性质知,BE=BC=
,
则在Rt△ABE中,根据勾股定理知AE=
=
.
过D点作DH⊥AE于H,则S△ADE=
AD•BE=
×1×
=
,
又S△ADE=
AE•DH=
×
DH=
,
DH=
=
,
∴在Rt△DHE′中,sinα=
=
.
故答案是:菱形;
.
 解:(1)如图1,∵D点是AB的中点,
解:(1)如图1,∵D点是AB的中点,∴在直角三角形ABC中,
∴CD=AD=BD,
根据平移的性质得到CF=BD,BF=CD,
∴CF=BD=BF=CD,
∴四边形CDBF是菱形;
(2)如图2,在Rt△ABC中,
∵∠A=60°,AC=1,
∴BC=AC•tan60°=
| 3 |
| AC |
| cos60° |
根据旋转的性质知,BE=BC=
| 3 |
则在Rt△ABE中,根据勾股定理知AE=
| AB2+BE2 |
| 7 |
过D点作DH⊥AE于H,则S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
又S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| ||
| 2 |
DH=
| ||
|
| ||
| 7 |
∴在Rt△DHE′中,sinα=
| DH |
| DE |
| ||
| 14 |
故答案是:菱形;
| ||
| 14 |
点评:此题主要考查了锐角三角函数关系以及相似三角形的判定与性质和菱形的判定以及三角形面积求法等知识,利用平移性质得出对应边之间的关系是解题关键.

练习册系列答案
相关题目
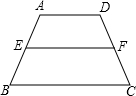 (2013•惠安县质检)如图,在梯形ABCD中,E、F分别为AB、CD边上的中点,AD=3,BC=5.则EF的长为
(2013•惠安县质检)如图,在梯形ABCD中,E、F分别为AB、CD边上的中点,AD=3,BC=5.则EF的长为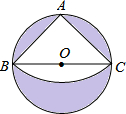 (2013•惠安县质检)如图所示,有一个直径是2米的圆形铁皮,从中剪出一个扇形ABC,其中BC是⊙O的直径.那么被剪掉的阴影部分面积=
(2013•惠安县质检)如图所示,有一个直径是2米的圆形铁皮,从中剪出一个扇形ABC,其中BC是⊙O的直径.那么被剪掉的阴影部分面积=