题目内容
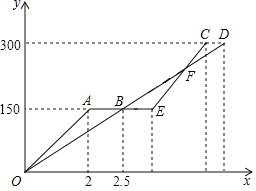
【题目】如图![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
![]() 求
求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
![]() 若点
若点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,连接
点,连接![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
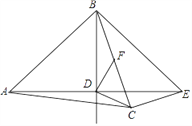
![]() 如图
如图![]() ,连接
,连接![]() ,
,![]() 及
及![]() ,设点
,设点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上任意一点,将
上任意一点,将![]() 沿边
沿边![]() 翻折得到
翻折得到![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
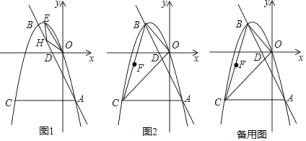
【答案】(1)点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
【解析】
(1)列方程组可知A、B两点坐标,根据点C的纵坐标与点A的纵坐标相同,列方程可求得点C坐标.
(2)如图1中,设![]() ,
,![]() ,则
,则![]() ,根据
,根据![]() 列出方程求出点H的横坐标,根据三角形的面积公式计算即可解决问题.
列出方程求出点H的横坐标,根据三角形的面积公式计算即可解决问题.
(3)分两种情形①若翻折后,点G在直线OC下方时,连接CG.如图2,可证四边形PFCG是平行四边形,得![]() ,在Rt△PBO中,根据
,在Rt△PBO中,根据![]() ,即可解决问题.②若翻折后,点G在直线OC上方时,连接CG.如图3,可证四边形PFGC是平行四边形,得
,即可解决问题.②若翻折后,点G在直线OC上方时,连接CG.如图3,可证四边形PFGC是平行四边形,得![]() 即可解决问题.
即可解决问题.
解:![]() 由
由![]() 解得
解得![]() 或
或![]() ,
,
∴点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,
,
∵![]() 轴,
轴,
∴点![]() 纵坐标为
纵坐标为![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ,
,
∴点![]() 坐标
坐标![]() .
.
![]() 如图
如图![]() 中,设
中,设![]() ,
,![]() ,则
,则![]() ,
,
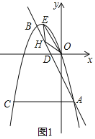
由题意![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
∴![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
①若翻折后,点![]() 在直线
在直线![]() 下方时,连接
下方时,连接![]() .如图
.如图![]() ,
,
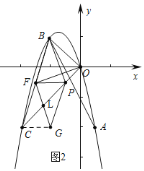
∵![]() ,
,
∴![]() ,
,
∴![]() .
.![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
②若翻折后,点![]() 在直线
在直线![]() 上方时,连接
上方时,连接![]() .如图
.如图![]() ,
,
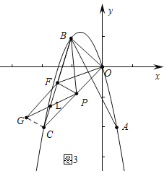
∵![]() ,
,
∴![]() ,
,
∴![]() .
.![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
综上所述:当![]() 或
或![]() 时,
时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.

练习册系列答案
相关题目