题目内容
如图,矩形ABCD中,AD=6,AB=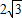 ,点O是AD的中点,点P在DA的延长线上,且AP=3.一动点E从P点出发,以每秒1个单位长度的速度沿射线PD匀速运动;另一动点F从D点出发,以每秒1个单位长度的速度沿DO匀速运动,到达O点后,立即以原速度沿OD返回.已知点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PD的同侧,设运动的时间为t秒(t≥0).
,点O是AD的中点,点P在DA的延长线上,且AP=3.一动点E从P点出发,以每秒1个单位长度的速度沿射线PD匀速运动;另一动点F从D点出发,以每秒1个单位长度的速度沿DO匀速运动,到达O点后,立即以原速度沿OD返回.已知点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PD的同侧,设运动的时间为t秒(t≥0).(1)当等边△EFG的边EG恰好经过点B时,运动时间t的值为______;
(2)当等边△EFG的顶点G恰好落在BC上时,运动时间t的值为______;
(3)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请写出S与t 之间的函数关系式和相应的自变量t的取值范围.
【答案】分析:(1)当边EG恰好经过点B时,∠DEB=60°,AE=3-t,在Rt△DEB中,解直角三角形可求t的值;
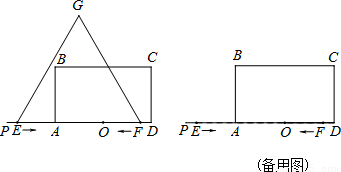
(2)当等边△EFG的顶点G恰好落在BC上时,等边△EFG的高=AB=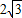 ,可求此时等边△EFG的边长,从而可求t的值;
,可求此时等边△EFG的边长,从而可求t的值;
(3)按照等边△EFG和矩形ABCD重叠部分的图形特点,分为0≤t<1,1≤t<2.5,2.5<t<3,3≤t<6,6≤t<7.5五种情况,分别写出函数关系式.
解答: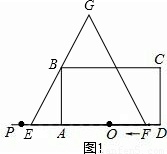 解:(1)∵△GEF是等边三角形,
解:(1)∵△GEF是等边三角形,
∴∠GED=60°,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠BAE=90°,
∴∠ABE=30°.
∴tan∠ABE=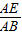 =
=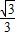 .
.
设PE=t,则AE=3-t,
∴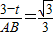 .
.
∵AB=2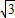 ,
,
∴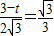 ,
,
∴t=1.
故答案为:1s;
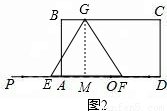
(2)如图2,设t秒后等边△EFG的顶点G恰好落在BC上,作GM⊥PD于M,
在Rt△EGM中,由勾股定理得:
EM=2,
∴EF=4,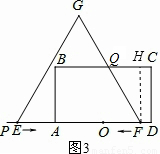
∴9-2t=4,
∴t=2.5s.
故答案为:2.5.
(3)①当0≤t<1时,重合部分是直角梯形,如图3,作FH⊥BC与H,
DF=CH=t,则在直角△FQH中,QH=HF•tan30°=2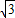 ×
×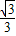 =2,
=2,
则BQ=BC-QH-CH=6-2-t=4-t,
∴S= (BQ+AF)•AB=
(BQ+AF)•AB= (4-t+6-t)•2
(4-t+6-t)•2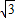 =-2
=-2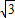 t+10
t+10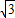 ;
;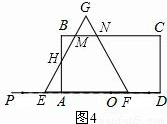
②当1≤t<2.5时,如图4,同上可得:CN=2+t,
BM=t-2.5,
则MN=6-(2+t)-(t-2.5)=6.5-2t,
EF=6+3-2t=9-2t,AE=3-t,
则S△AEH= AE•AH=
AE•AH= ×(3-t)•
×(3-t)•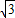 (3-t)2=
(3-t)2=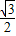 (3-t)2;
(3-t)2;
S△EFG=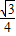 (9-2t)2,S△MNG=
(9-2t)2,S△MNG=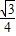 (6.5-t)2,
(6.5-t)2,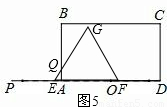
则重合部分的面积是:S=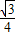 (9-2t)2-
(9-2t)2-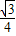 (6.5-t)2-
(6.5-t)2-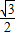 (3-t)2;
(3-t)2;
③当2.5<t<3时,如图5,
等边△EFG的边长是9-2t,则面积是: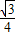 (9-2t)2,
(9-2t)2,
直角△AEQ中,AE=3-t,则AQ=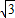 (3-t),
(3-t),
因而△AEQ的面积是: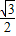 (3-t)2,
(3-t)2,
则S=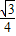 (9-2t)2-
(9-2t)2-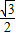 (3-t)2;
(3-t)2;
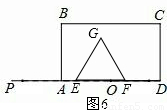
④当3≤t<6时,如图6,重合部分就是△EFG,边长是:3,则S=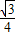 ×32=
×32=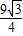 ;
;
⑤当6≤t<7.5时,如图7,重合部分就是△EFG,边长是:3-2t,
则S=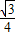 (3-2t)2.
(3-2t)2.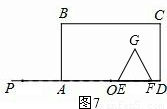
点评:本题是函数与矩形、三角形的面积的计算,正确分情况讨论是解题的关键.
(2)当等边△EFG的顶点G恰好落在BC上时,等边△EFG的高=AB=
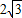 ,可求此时等边△EFG的边长,从而可求t的值;
,可求此时等边△EFG的边长,从而可求t的值;(3)按照等边△EFG和矩形ABCD重叠部分的图形特点,分为0≤t<1,1≤t<2.5,2.5<t<3,3≤t<6,6≤t<7.5五种情况,分别写出函数关系式.
解答:
 解:(1)∵△GEF是等边三角形,
解:(1)∵△GEF是等边三角形,∴∠GED=60°,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠BAE=90°,
∴∠ABE=30°.
∴tan∠ABE=
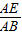 =
=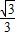 .
.设PE=t,则AE=3-t,
∴
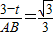 .
.
∵AB=2
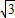 ,
,∴
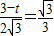 ,
,∴t=1.
故答案为:1s;
(2)如图2,设t秒后等边△EFG的顶点G恰好落在BC上,作GM⊥PD于M,
在Rt△EGM中,由勾股定理得:
EM=2,
∴EF=4,

∴9-2t=4,
∴t=2.5s.
故答案为:2.5.
(3)①当0≤t<1时,重合部分是直角梯形,如图3,作FH⊥BC与H,
DF=CH=t,则在直角△FQH中,QH=HF•tan30°=2
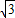 ×
×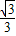 =2,
=2,则BQ=BC-QH-CH=6-2-t=4-t,
∴S=
 (BQ+AF)•AB=
(BQ+AF)•AB= (4-t+6-t)•2
(4-t+6-t)•2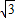 =-2
=-2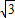 t+10
t+10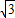 ;
;
②当1≤t<2.5时,如图4,同上可得:CN=2+t,
BM=t-2.5,
则MN=6-(2+t)-(t-2.5)=6.5-2t,
EF=6+3-2t=9-2t,AE=3-t,
则S△AEH=
 AE•AH=
AE•AH= ×(3-t)•
×(3-t)•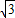 (3-t)2=
(3-t)2=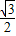 (3-t)2;
(3-t)2;S△EFG=
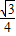 (9-2t)2,S△MNG=
(9-2t)2,S△MNG=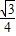 (6.5-t)2,
(6.5-t)2,
则重合部分的面积是:S=
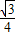 (9-2t)2-
(9-2t)2-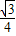 (6.5-t)2-
(6.5-t)2-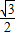 (3-t)2;
(3-t)2;③当2.5<t<3时,如图5,
等边△EFG的边长是9-2t,则面积是:
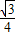 (9-2t)2,
(9-2t)2,直角△AEQ中,AE=3-t,则AQ=
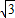 (3-t),
(3-t),因而△AEQ的面积是:
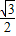 (3-t)2,
(3-t)2,则S=
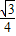 (9-2t)2-
(9-2t)2-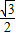 (3-t)2;
(3-t)2;④当3≤t<6时,如图6,重合部分就是△EFG,边长是:3,则S=
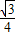 ×32=
×32=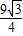 ;
;
⑤当6≤t<7.5时,如图7,重合部分就是△EFG,边长是:3-2t,
则S=
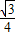 (3-2t)2.
(3-2t)2.
点评:本题是函数与矩形、三角形的面积的计算,正确分情况讨论是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
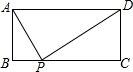 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
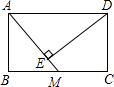 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.