题目内容
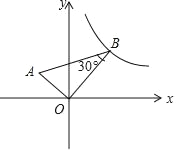
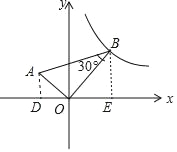
【题目】如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=![]() 的图象上,求过点A的反比例函数的解析式.
的图象上,求过点A的反比例函数的解析式.
【答案】反比例函数的解析式为y=﹣![]() .
.
【解析】试题分析:
如图,作AD⊥x轴于D,BE⊥x轴于E,由点B在![]() 的图象上,可设其坐标为B(m,
的图象上,可设其坐标为B(m, ![]() ),则OE=m,BE=
),则OE=m,BE=![]() ,在Rt△AOB中,由∠B=30°可得OB=
,在Rt△AOB中,由∠B=30°可得OB=![]() OA,再证△AOD∽△OBE,即可由相似三角形的性质把OD、AD用含“m”的代数式表达出来,从而可表达出点A的坐标,这样即可求得过点A的反比例函数的解析式了.
OA,再证△AOD∽△OBE,即可由相似三角形的性质把OD、AD用含“m”的代数式表达出来,从而可表达出点A的坐标,这样即可求得过点A的反比例函数的解析式了.
试题解析:
作AD⊥x轴于D,BE⊥x轴于E,如图,设B(m, ![]() )
)
在Rt△ABO中,∵∠B=30°,
∴OB=![]() OA,
OA,
∵∠AOD=∠OBE,
∴Rt△AOD∽Rt△OBE,
∴![]() ,即
,即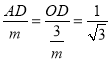 ,
,
∴AD= ![]() ,OD=
,OD=![]() ,
,
∴A点坐标为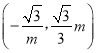 ,
,
设点A所在反比例函数的解析式为![]() ,
,
∴k=![]() ,
,
∴点B所在反比例函数的解析式为![]() .
.

练习册系列答案
相关题目