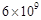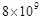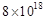��Ŀ����
��2011�Ĵ��ڽ�������5��12�֣�ͬѧ�ǣ����������о���n��n�����������õ��������������ε������ı���ʽΪ12+22+32+��+n2����nΪ100ʱ��Ӧ��μ��������εľ��������?�������Ǿ�һ����̽�������������⣮���ȣ�ͨ��̽�������Ѿ�֪��0��1+1��2+2��3+��+(n��1)��n= n(n+1)(n��1)ʱ�����ǿ�����������
n(n+1)(n��1)ʱ�����ǿ�����������
(1)�۲첢���룺
12+22=(1+0)��1+(1+1)��2=1+0��1+2+1��2=(1+2)+(0��1+1��2)
12+22+32=(1+0)��1+(1+1)��2+(1+2)��3
=1+0��1+2+1��2+3+2��3
=(1+2+3)+(0��1+1��2+2��3)
12+22+32+42=(1+0)��1+(1+1)��2+(1+2)��3+
=1+0��1+2+1��2+3+2��3+
=(1+2+3+4)+( )
����
(2)���ɽ��ۣ�
12+22+32+��+n2=(1+0)��1+(1+1)��2+(1+2)��3+��+n
=1+0��1+2+1��2+3+2��3+��+n+(nһ1)��n
=( ) +
= +
= ��
��
(3)ʵ��Ӧ�ã�
ͨ������̽�����̣����ǾͿ��������nΪ100ʱ�������������������ε��ܸ����� ��
 n(n+1)(n��1)ʱ�����ǿ�����������
n(n+1)(n��1)ʱ�����ǿ�����������(1)�۲첢���룺
12+22=(1+0)��1+(1+1)��2=1+0��1+2+1��2=(1+2)+(0��1+1��2)
12+22+32=(1+0)��1+(1+1)��2+(1+2)��3
=1+0��1+2+1��2+3+2��3
=(1+2+3)+(0��1+1��2+2��3)
12+22+32+42=(1+0)��1+(1+1)��2+(1+2)��3+
=1+0��1+2+1��2+3+2��3+
=(1+2+3+4)+( )
����
(2)���ɽ��ۣ�
12+22+32+��+n2=(1+0)��1+(1+1)��2+(1+2)��3+��+n
=1+0��1+2+1��2+3+2��3+��+n+(nһ1)��n
=( ) +
= +
=
 ��
�� (3)ʵ��Ӧ�ã�
ͨ������̽�����̣����ǾͿ��������nΪ100ʱ�������������������ε��ܸ����� ��
��1+3����4
4+3��4
0��1+1��2+2��3+3��4
1+2+3+��+n
0��1+1��2+2��3++��+(n��1)��n
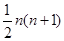
 n(n+1)(n��1)
n(n+1)(n��1)
n(n+1)(2n+1)
4+3��4
0��1+1��2+2��3+3��4
1+2+3+��+n
0��1+1��2+2��3++��+(n��1)��n
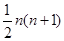
 n(n+1)(n��1)
n(n+1)(n��1)n(n+1)(2n+1)
��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
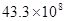
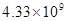
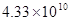
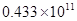
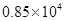 ��Ԫ
��Ԫ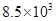 ��Ԫ
��Ԫ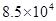 ��Ԫ
��Ԫ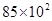 ��Ԫ
��Ԫ

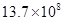
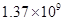
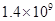
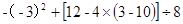
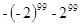
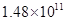
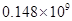
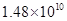
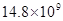
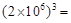 �� ��
�� ��