题目内容
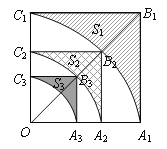
【题目】如图,正方形![]() 的边长为1,以
的边长为1,以![]() 为圆心、
为圆心、![]() 为半径作扇形OA1C1弧A1C1与
为半径作扇形OA1C1弧A1C1与![]() 相交于点
相交于点![]() ,设正方形
,设正方形![]() 与扇形
与扇形![]() 之间的阴影部分的面积为
之间的阴影部分的面积为![]() ;然后以
;然后以![]() 为对角线作正方形
为对角线作正方形![]() ,又以
,又以![]() 为圆心,、
为圆心,、![]() 为半径作扇形
为半径作扇形![]() ,弧A2C2与
,弧A2C2与![]() 相交于点
相交于点![]() ,设正方形
,设正方形![]() 与扇形
与扇形![]() 之间的阴影部分面积为
之间的阴影部分面积为![]() ;按此规律继续作下去,设正方形
;按此规律继续作下去,设正方形![]() 与扇形
与扇形![]() 之间的阴影部分面积为
之间的阴影部分面积为![]() .
.
(1)求![]() ;
;
(2)写出![]() ;
;
(3)试猜想![]() (用含
(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数).
为正整数).
【答案】(1)S1=1-![]() π,S2=
π,S2=![]() -
-![]() ,S3=
,S3=![]() -
-![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (n为正整数).
(n为正整数).
【解析】
试题分析:根据阴影部分的面积是正方形的面积减去所对应的扇形的面积可求解,所以可分别计算出S1=1-![]() π,S2=
π,S2=![]() -
-![]() ,S3=
,S3=![]() -
-![]() ;那么Sn=
;那么Sn=![]() -
-![]() (n为正整数).可据此求出当n=2008时,S的值.
(n为正整数).可据此求出当n=2008时,S的值.
试题解析:(1)S1=12-![]()
![]() π
π![]() 12=1-
12=1-![]() π;
π;
由勾股定理得:OA22+A2B22=OB22=12,
∴OA2=![]() ,
,
S2=(![]() )2-
)2-![]()
![]() π
π![]() (
(![]() )2=
)2=![]() -
-![]() ;
;
S3=(![]() ×
×![]() )2-
)2-![]()
![]() π
π![]() (
(![]() ×
×![]() )2=
)2=![]() -
-![]() ;
;
(2)S2008=![]() ;
;
(3)Sn=![]() (n为正整数).
(n为正整数).

练习册系列答案
相关题目