题目内容
【题目】先化简，再求值：2（x2-2xy）-3（-xy-x2）-xy，其中x，y满足|x+1|+（y-2）2=0
【答案】5x2-2xy，9.
【解析】
首先去括号进而合并同类项，再把已知数据代入求出答案．
解：原式=2x2-4xy+3xy+3x2-xy=5x2-2xy，
∵|x+1|+（y-2）2=0，
∴x+1=0，y-2=0，
解得：x=-1，y=2，
故原式=5×（-1）2-2×（-1）×2=9．
练习册系列答案
阅读快车系列答案
相关题目
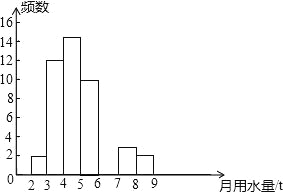
【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）
月均用水量（单位：t） | 频数 | 百分比 |
2≤x＜3 | 2 | 4% |
3≤x＜4 | 12 | 24% |
4≤x＜5 | a | b |
5≤x＜6 | 10 | 20% |
6≤x＜7 | c | 12% |
7≤x＜8 | 3 | 6% |
8≤x＜9 | 2 | 4% |
（1）频数分布表中a= ，b= ．（填百分比），c= ；补全频数分布直方图．
（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有 户；
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．
