题目内容
【题目】已知：△ABC中，BO平分∠ABC，CO平分∠ACB
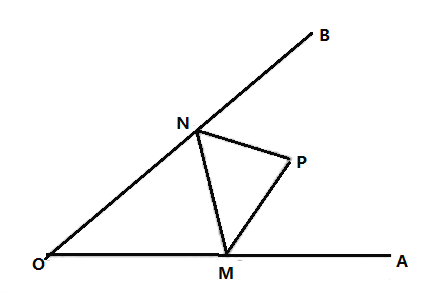
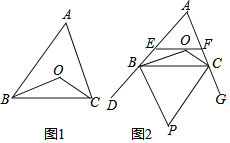
（1）如图1，∠BOC和∠A有怎样的数量关系？请说明理由
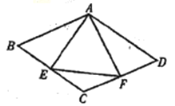
（2）如图2，过O点的直线分别交△ABC的边AB、AC于E、F（点E不与A，B重合，点F不与A、C重合），BP平分外角∠DBC，CP平分外角∠GCB，BP，CP相交于P．求证：∠P＝∠BOE+∠COF；
（3）如果（2）中过O点的直线与AB交于E（点E不与A、B重合），与CA的延长线交于F在其它条件不变的情况下，请直接写出∠P、∠BOE、∠COF三个角之间的数量关系．
【答案】（1）∠BOC＝90°+
∠A，理由详见解析；（2）详见解析；（3）∠BOE+∠COF﹣∠P＝180°．
【解析】
（1）根据三角形的内角和等于180°求出∠ABC+∠ACB的度数，再根据角平分线的定义求出∠OBC+∠OCB的度数，然后利用三角形的内角和等于180°列式计算即可得解；
（2）证明∠P＝90°﹣∠A，得到∠P+∠BOC＝180°即可解决问题；
（3）画出图形由∠P+∠BOC＝180°，∠BOC+∠BOE+∠COF＝360°，可得∠BOE+∠COF﹣∠P＝180°．
解：（1）∵∠ABC+∠ACB＝180°﹣∠A，BO平分∠ABC，CO平分∠ACB，
∴∠OBC＝∠ABC，∠OCB＝∠ACB，
∴∠OBC+∠OCB
＝（∠ABC+∠ACB）
＝（180°﹣∠A）
＝90°﹣∠A，
在△OBC中，∠BOC＝180°﹣（∠OBC+∠OCB）＝90°+∠A；
（2）∵BP、CP分别平分外角∠DBC、∠GCB，
∴∠PBC＝∠CBD，∠PCB＝∠BCG，
∴∠P＝180°﹣∠CBP﹣∠BCP）
＝180°﹣（∠CBD+∠BCG）
＝180°﹣（∠A+∠ACB+∠A+∠ABC）
＝180°﹣（180°+∠A）
＝90°﹣∠A，
∴∠P+∠BOC＝180°，
∵∠BOC+∠BOE+∠COF＝180°，
∴∠P＝∠BOE+∠COF；
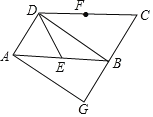
（3）如图3中，
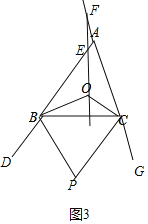
∵∠P+∠BOC＝180°，∠BOC+∠BOE+∠COF＝360°，
∴∠BOE+∠COF﹣∠P＝180°．
