题目内容
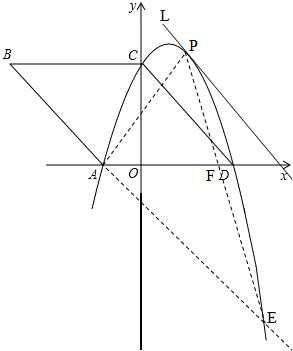
如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB= .
.
(1)求过A.C. D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
 .
.(1)求过A.C. D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.

解:(1)∵四边形ABCD是菱形,
∴AB=AD=CD=BC=5,sinB=sinD=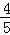 ;
;
Rt△OCD中,OC=CD•sinD=4,OD=3;
OA=AD﹣OD=2,即:
A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);
设抛物线的解析式为:y=a(x+2)(x﹣3),得:
2×(﹣3)a=4,a=﹣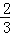 ;
;
∴抛物线:y=﹣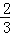 x2+
x2+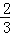 x+4.
x+4.
(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣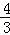 x﹣
x﹣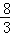 ;
;
由(1)得:y2=﹣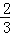 x2+
x2+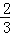 x+4,则:
x+4,则:
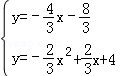 ,解得:
,解得: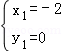 ,
,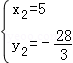 ;
;
由图可知:当y1<y2时,﹣2<x<5.
(3)∵S△APE= AE•h,
AE•h,
∴当P到直线AB的距离最远时,S△ABC最大;
若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;
设直线L:y=﹣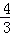 x+b,当直线L与抛物线有且只有一个交点时,
x+b,当直线L与抛物线有且只有一个交点时,
﹣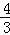 x+b=﹣
x+b=﹣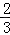 x2+
x2+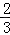 x+4,且△=0;
x+4,且△=0;
求得:b=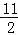 ,即直线L:y=﹣
,即直线L:y=﹣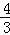 x+
x+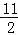 ;
;
可得点P(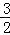 ,
,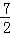 ).
).
由(2)得:E(5,﹣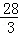 ),则直线PE:y=﹣
),则直线PE:y=﹣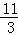 x+9;
x+9;
则点F( ,0),AF=OA+OF=
,0),AF=OA+OF=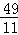 ;
;
∴△PAE的最大值:S△PAE=S△PAF+S△AEF= ×
×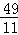 ×(
×(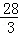 +
+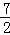 )=
)=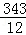 .
.
综上所述,当P(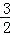 ,
,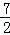 )时,△PAE的面积最大,为
)时,△PAE的面积最大,为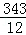 .
.
∴AB=AD=CD=BC=5,sinB=sinD=
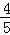 ;
;Rt△OCD中,OC=CD•sinD=4,OD=3;
OA=AD﹣OD=2,即:
A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);
设抛物线的解析式为:y=a(x+2)(x﹣3),得:
2×(﹣3)a=4,a=﹣
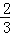 ;
;∴抛物线:y=﹣
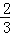 x2+
x2+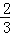 x+4.
x+4.(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣
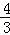 x﹣
x﹣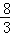 ;
;由(1)得:y2=﹣
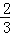 x2+
x2+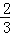 x+4,则:
x+4,则: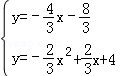 ,解得:
,解得: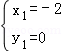 ,
,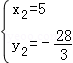 ;
;由图可知:当y1<y2时,﹣2<x<5.
(3)∵S△APE=
 AE•h,
AE•h,∴当P到直线AB的距离最远时,S△ABC最大;
若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;
设直线L:y=﹣
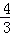 x+b,当直线L与抛物线有且只有一个交点时,
x+b,当直线L与抛物线有且只有一个交点时,﹣
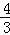 x+b=﹣
x+b=﹣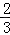 x2+
x2+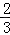 x+4,且△=0;
x+4,且△=0;求得:b=
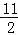 ,即直线L:y=﹣
,即直线L:y=﹣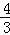 x+
x+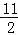 ;
;可得点P(
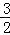 ,
,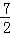 ).
).由(2)得:E(5,﹣
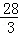 ),则直线PE:y=﹣
),则直线PE:y=﹣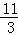 x+9;
x+9;则点F(
 ,0),AF=OA+OF=
,0),AF=OA+OF=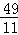 ;
;∴△PAE的最大值:S△PAE=S△PAF+S△AEF=
 ×
×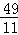 ×(
×(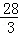 +
+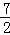 )=
)=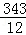 .
.综上所述,当P(
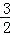 ,
,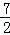 )时,△PAE的面积最大,为
)时,△PAE的面积最大,为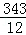 .
.
(1)由菱形ABCD的边长和一角的正弦值,可求出OC.OD.OA的长,进而确定A.C.D三点坐标,通过待定系数法可求出抛物线的解析式.
(2)首先由A.B的坐标确定直线AB的解析式,然后求出直线AB与抛物线解析式的两个交点,然后通过观察图象找出直线y1在抛物线y2图象下方的部分.
(3)该题的关键点是确定点P的位置,△APE的面积最大,那么S△APE= AE×h中h的值最大,即点P离直线AE的距离最远,那么点P为与直线AB平行且与抛物线有且仅有的唯一交点.
AE×h中h的值最大,即点P离直线AE的距离最远,那么点P为与直线AB平行且与抛物线有且仅有的唯一交点.
(2)首先由A.B的坐标确定直线AB的解析式,然后求出直线AB与抛物线解析式的两个交点,然后通过观察图象找出直线y1在抛物线y2图象下方的部分.
(3)该题的关键点是确定点P的位置,△APE的面积最大,那么S△APE=
 AE×h中h的值最大,即点P离直线AE的距离最远,那么点P为与直线AB平行且与抛物线有且仅有的唯一交点.
AE×h中h的值最大,即点P离直线AE的距离最远,那么点P为与直线AB平行且与抛物线有且仅有的唯一交点.
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的解是
的解是 ,求
,求

 (2)
(2)

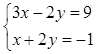
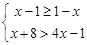 的整数解;
的整数解;