题目内容
 (2012•海陵区二模)如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
(2012•海陵区二模)如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )分析:过A作AE⊥l3于E,过C作CF⊥l3于F,求出∠AEB=∠CFB,∠EAB=∠CBF,根据AAS证△AEB≌△BFC,推出AE=BF=2,BE=CF=3,由勾股定理求出AB和BC,再由勾股定理求出AC即可.
解答:解: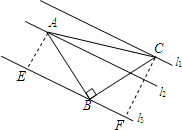
过A作AE⊥l3于E,过C作CF⊥l3于F,
则∠AEF=∠CFB=∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∠EAB+∠ABE=90°,
∴∠EAB=∠CBF,
∵在△AEB和△BFC中
,
∴△AEB≌△BFC(AAS),
∴AE=BF=2,BE=CF=2+1=3,
由勾股定理得:AB=BC=
=
,
由勾股定理得:AC=
=
,
故选C.

过A作AE⊥l3于E,过C作CF⊥l3于F,
则∠AEF=∠CFB=∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∠EAB+∠ABE=90°,
∴∠EAB=∠CBF,
∵在△AEB和△BFC中
|
∴△AEB≌△BFC(AAS),
∴AE=BF=2,BE=CF=2+1=3,
由勾股定理得:AB=BC=
| 22+32 |
| 13 |
由勾股定理得:AC=
(
|
| 26 |
故选C.
点评:本题考查的知识点有两平行线间的距离,全等三角形的性质和判定,勾股定理,解此题的关键是构造全等三角形求出AB和BC的长.

练习册系列答案
相关题目