题目内容
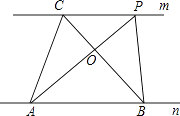
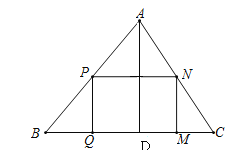
【题目】如图，△ABC是一块锐角三角形的余料，它的边BC=120mm，高AD=80mm．要把它加工成一个矩形零件PQMN，使矩形的一边在BC上，其余两个顶点分别在AB，AC上．问要使加工成的这个矩形面积最大，那么边长MN应是多少mm？
【答案】40mm.
【解析】试题分析：设矩形的一边PQ为x mm，另一边PN为y mm，由△APN∽△ABC，得
，可得y与x的函数解析式，进一步可得S=xy，转化为S关于x的二次函数，把求矩形面积的最值转化为求二次函数的最值即可.
试题解析：设AD交PN于点E.
∵四边形PQMN是矩形，AD⊥BC
∴PN∥BC, AD⊥PN,DE=MN
∴△APN∽△ABC
∴
设MN=x，PN=y，矩形PQMN的面积为S，由条件可得
解得
．
∴
∵
∴当x=40时S取最大值
所以要使加工成的这个矩形面积最大，边长MN应是40mm.
练习册系列答案
同步练习强化拓展系列答案
相关题目
【题目】某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
（1） 表中a＝__________，b＝__________，c＝__________
（2） 请补全频数分布直方图
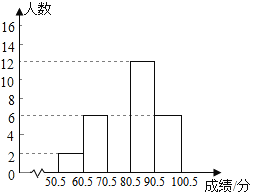
（3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
