题目内容
 如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是
如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是
- A.3
- B.4
- C.5
- D.7
A
分析:根据矩形的性质和EF⊥EC,EF=EC求证△AEF≌△DCE,可得AE=CD,再利用矩形的周长为16,即可求出AD,然后用AD减DE即可得出答案.
解答:∵矩形ABCD中,EF⊥EC,
∴∠DEC+∠DCE=90°,∠DEC+∠AEF=90°
∴∠AEF=∠DCE,
又∵EF=EC,
∴△AEF≌△DCE,
∴AE=CD,
∵矩形的周长为16,即2CD+2AD=16,
∴CD+AD=8,
∴AD-2+AD=8,
AD=5,
∴AE=AD-DE=5-2=3.
故选A.
点评:此题主要考查学生对全等三角形的判定与性质和矩形性质的理解和掌握,解答此题的关键是求证△AEF≌△DCE.
分析:根据矩形的性质和EF⊥EC,EF=EC求证△AEF≌△DCE,可得AE=CD,再利用矩形的周长为16,即可求出AD,然后用AD减DE即可得出答案.
解答:∵矩形ABCD中,EF⊥EC,
∴∠DEC+∠DCE=90°,∠DEC+∠AEF=90°
∴∠AEF=∠DCE,
又∵EF=EC,
∴△AEF≌△DCE,
∴AE=CD,
∵矩形的周长为16,即2CD+2AD=16,
∴CD+AD=8,
∴AD-2+AD=8,
AD=5,
∴AE=AD-DE=5-2=3.
故选A.
点评:此题主要考查学生对全等三角形的判定与性质和矩形性质的理解和掌握,解答此题的关键是求证△AEF≌△DCE.

练习册系列答案
相关题目
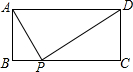 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
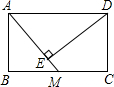 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为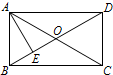 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为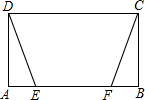 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.