Question

【题目】如图，已知 为 上的一点，按下列要求进行作图．

（1）作 的平分线 .
（2）在 上取一点 ，使得 .
（3）爱动脑筋的小刚经过仔细观察后，进行如下操作：在边 上取一点 ，使得 ，这时他发现 与 之间存在一定的数量关系，请写出 与 的数量关系，并说明理由．

Answer 1

【答案】
（1）解：如图，OC即为所求；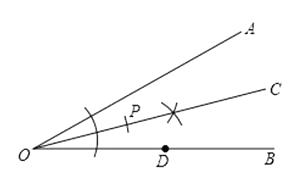
（2）解：如图，OP=a

（3）解：∠OEP=∠ODP或∠OEP+∠ODP=180°． 理由是：以O为圆心，以OD为半径作弧，交OA于E2 ， 连接PE2 ， 作PM⊥OA于M， PN⊥OB于N，则PM=PN． 在△E2PM和△DPN中， ， ∴△E2PM≌△DPN（HL）， ∴∠OE2P=∠ODP； 以P为圆心，以PD为半径作弧，交OA于另一点E1 ， 连接PE1 ， 则此点E1也符合条件PD=PE1 ，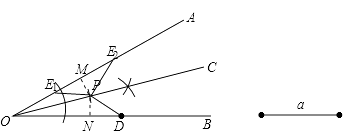

∵PE2=PE1=PD， ∴∠PE2E1=∠PE1E2 ， ∵∠OE1P+∠E2E1P=180°， ∵∠OE2P=∠ODP， ∴∠OE1P+∠ODP=180°， ∴∠OEP与∠ODP所有可能的数量关系是：∠OEP=∠ODP或∠OEP+∠ODP=180°
【解析】（1）利用尺规作图按要求画出图形即可。
（2）在 OC 上取一点 P ，使得 OP=a 即可。
（3）以O为圆心，以OD为半径作弧，交OA于E2，连接PE2，作PM⊥OA于M， PN⊥OB于N，根据角平分线的性质得出PM=PN，再证明△E2PM≌△DPN，得出∠OE2P=∠ODP，再根据角平分线的定义即可得出 ∠OEP 与 ∠ODP 的数量关系。