题目内容
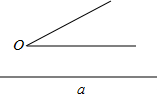 如图,已知线段a及∠O.
如图,已知线段a及∠O.(1)只用直尺和圆规,求作△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法);
(2)在△ABC中作BC的中垂线分别交AB、BC于点E、F,如果∠B=30°,求△ABC面积被中垂线分成的两部分之比.
分析:(1)先作一个角等于已知角,即∠CBA=∠O,截取BC=a,以射线CB为一边,C为顶点,作∠ACB=2∠O,△ABC即为所求;
(2)由∠B=30°,可得∠ACB=60°,根据三角函数可求得AB的长,则△ABC∽△FBE,从而得出
=
,根据相似三角形的面积比等于相似比的平方,求得答案即可.
(2)由∠B=30°,可得∠ACB=60°,根据三角函数可求得AB的长,则△ABC∽△FBE,从而得出
| BF |
| AB |
| 1 | ||
|
解答: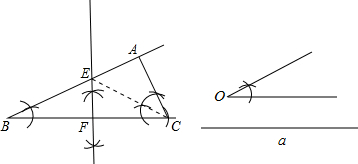 解:(1)作三角形图---------------------------(4分);
解:(1)作三角形图---------------------------(4分);
(分解:作已知角、2倍角、取BC=a、完成三角形各1分)
(2)作BC中垂线,连接EC,
∵∠B=30°,∠ACB=2∠B=60°,
∴∠BAC=90°,
∵∠BFE=90°,
∴△ABC∽△FBE,
∵BC=a,
∴AB=
a,
∴
=
=
,
∴S△BEF:S△ABC=1:3,
∴△FEC≌△AEC,
所以△BEF与四边形AEFC的面积之比为1:2.
 解:(1)作三角形图---------------------------(4分);
解:(1)作三角形图---------------------------(4分);(分解:作已知角、2倍角、取BC=a、完成三角形各1分)
(2)作BC中垂线,连接EC,
∵∠B=30°,∠ACB=2∠B=60°,
∴∠BAC=90°,
∵∠BFE=90°,
∴△ABC∽△FBE,
∵BC=a,
∴AB=
| ||
| 2 |
∴
| BF |
| AB |
| ||||
|
| 1 | ||
|
∴S△BEF:S△ABC=1:3,
∴△FEC≌△AEC,
所以△BEF与四边形AEFC的面积之比为1:2.
点评:本题考查了基本作图,作一个角等于已知角,以及相似三角形的判定和性质,相似三角形的面积之比等于相似比的平方.

练习册系列答案
相关题目
 23、在方格纸上画图并回答问题.如图,已知线段AB及点C.
23、在方格纸上画图并回答问题.如图,已知线段AB及点C.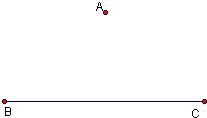 8、如图,已知线段BC及BC外一点A,以A点为顶点,BC为对角线可以作
8、如图,已知线段BC及BC外一点A,以A点为顶点,BC为对角线可以作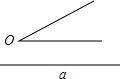 如图,已知线段a及∠O.
如图,已知线段a及∠O.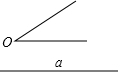 (2013•鞍山)如图,已知线段a及∠O,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)
(2013•鞍山)如图,已知线段a及∠O,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)