题目内容
（2006•湛江）如图，已知直线AB∥CD，∠ABE=60°，∠CDE=20°，则∠BED= 度．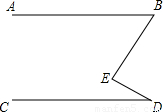
【答案】分析：根据两直线平行，内错角相等求出∠EFD，再根据三角形外角等于和它不相邻的两个内角和即可解答．
解答：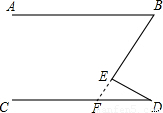
解：∵AB∥CD，
∴∠EFD=∠ABE=60°，
在△EFD中，根据三角形的外角性质得到
∠BED=∠EFD+∠CDE=80°，即∠BED=80°．
点评：本题考查了三角形的外角的性质，外角等于不相邻的两个外角的和；平行线的性质，两直线平行，内错角相等．
解答：
解：∵AB∥CD，∴∠EFD=∠ABE=60°，
在△EFD中，根据三角形的外角性质得到
∠BED=∠EFD+∠CDE=80°，即∠BED=80°．
点评：本题考查了三角形的外角的性质，外角等于不相邻的两个外角的和；平行线的性质，两直线平行，内错角相等．
练习册系列答案
名校课堂系列答案
相关题目
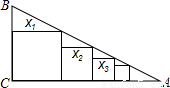
（2006•湛江）如图，在Rt△ABC中，∠C=90°，BC=1，AC=2，把边长分别为x1，x2，x3，…，xn的n个正方形依次放入△ABC中，请回答下列问题：
（1）按要求填表：
（2）第n个正方形的边长xn=______；
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．
（1）按要求填表：
| n | 1 | 2 | 3 |
| xn |
（3）若m，n，p，q是正整数，且xm•xn=xp•xq，试判断m，n，p，q的关系．
