题目内容
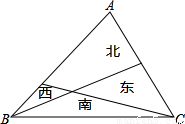
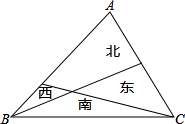某农场主有一块均匀种植的三角形草地，他把草地分成东、南、西、北4块如图，经过统计得出，在西边草地可牧5只羊，南边草地可牧10只羊，东边草地可牧8只羊，则北边草地可牧（ ）只羊．| A、13 | B、18 | C、22 | D、23 |
分析：将北边分割成东北和西北两块为x，y，则：北边可牧（x+y）只．
可以列出：
=
，
=
，求解即可．
可以列出：
| x+5 |
| y |
| 10 |
| 8 |
| y+8 |
| x |
| 10 |
| 5 |
解答：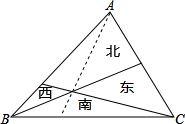
解：将北边分割成东北和西北两块为x，y，则：北边可牧（x+y）只．
可以列出：
=
，
=
解得：x=10，y=12
所以，北边可牧：10+12=22只．
故选C．
解：将北边分割成东北和西北两块为x，y，则：北边可牧（x+y）只．可以列出：
| x+5 |
| y |
| 10 |
| 8 |
| y+8 |
| x |
| 10 |
| 5 |
解得：x=10，y=12
所以，北边可牧：10+12=22只．
故选C．
点评：此类题利用列方程求解可简化计算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
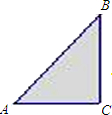某小区有一块直角三角形的绿地，量得两直角边AC=3米，BC=4米，考虑到这块绿地周围还有不少空余部分，于是打算将这块绿地扩充成等腰三角形，且扩充部分是以BC边为一直角边的直角三角形，求扩充后得到的等腰三角形绿地的周长（写出所有可能的情形）．
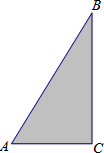某小区有一块直角三角形的绿地，量得两直角边AC=10米，BC=24米，考虑到这块绿地周围还有不少空余部分，于是打算将这块绿地扩充成等腰三角形，且扩充部分是以BC边为一直角边的直角三角形，求扩充后得到的等腰三角形绿地的面积（写出所有可能的情形）．
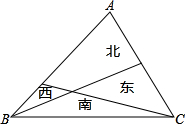某农场主有一块均匀种植的三角形草地，他把草地分成东、南、西、北4块如图，经过统计得出，在西边草地可牧5只羊，南边草地可牧10只羊，东边草地可牧8只羊，则北边草地可牧______只羊．