题目内容
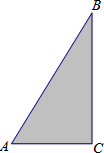 某小区有一块直角三角形的绿地,量得两直角边AC=10米,BC=24米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的面积(写出所有可能的情形).
某小区有一块直角三角形的绿地,量得两直角边AC=10米,BC=24米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的面积(写出所有可能的情形).分析:共三种情况:AB=BD,AB=AE,BF=AF,分别根据等腰三角形的性质计算出底边和高,然后再根据三角形的面积公式进行计算即可.
解答: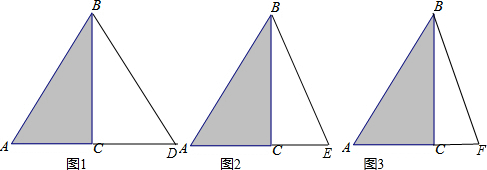 解:如图所示:
解:如图所示:
共三种情况:如图1,AB=BD,
△ABD的面积为
AD•BC=
×20×24=240(平方米);
如图2,AB=AE,
∵AC=10米,BC=24米,
∴AB=
=26米,
△ABE的面积为
AE•BC=
×26×24=312(平方米);
如图3,BF=AF,
设CF=x米,则BF=(10+x)米,
在直角三角形BCF中:x2+242=(10+x)2,
解得:x=23.8,
△ABE的面积为:
×33.8×24=405.6(平方米).
 解:如图所示:
解:如图所示:共三种情况:如图1,AB=BD,
△ABD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
如图2,AB=AE,
∵AC=10米,BC=24米,
∴AB=
| 676 |
△ABE的面积为
| 1 |
| 2 |
| 1 |
| 2 |
如图3,BF=AF,
设CF=x米,则BF=(10+x)米,
在直角三角形BCF中:x2+242=(10+x)2,
解得:x=23.8,
△ABE的面积为:
| 1 |
| 2 |
点评:此题主要考查了作图与应用设计作图,关键是考虑全面,进行分类讨论,不要漏解.

练习册系列答案
相关题目
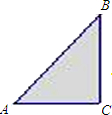 某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长(写出所有可能的情形).
某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长(写出所有可能的情形).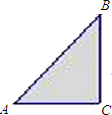 某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长(写出所有可能的情形).
某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长(写出所有可能的情形). 某小区有一块直角三角形的绿地,量得两直角边AC=10米,BC=24米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的面积(写出所有可能的情形).
某小区有一块直角三角形的绿地,量得两直角边AC=10米,BC=24米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的面积(写出所有可能的情形).