题目内容
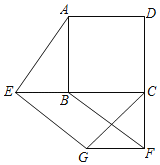
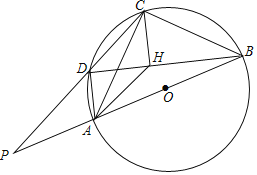
【题目】四边形![]() 是
是![]() 的圆内接四边形,线段
的圆内接四边形,线段![]() 是
是![]() 的直径,连结
的直径,连结![]() .点
.点![]() 是线段
是线段![]() 上的一点,连结
上的一点,连结![]() ,且
,且![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线相交与点
的延长线相交与点![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() ,
,![]()
①求证:![]() 为等腰直角三角形;
为等腰直角三角形;
②求![]() 的长度.
的长度.
【答案】(1)见解析;(2)①见解析;②![]() .
.
【解析】
(1)由圆周角的定理可得![]() ,可证
,可证![]() ,由一组对边平行且相等的是四边形是平行四边形可证四边形
,由一组对边平行且相等的是四边形是平行四边形可证四边形![]() 是平行四边形;
是平行四边形;
(2)①由平行线的性质可证![]() ,由
,由![]() ,可证
,可证![]() 为等腰直角三角形;
为等腰直角三角形;
②通过证明![]() ,可得
,可得![]() ,可得
,可得![]() ,通过证明
,通过证明![]() ,可得
,可得![]() ,可得
,可得![]() ,可求
,可求![]() ,由等腰直角三角形的性质可求
,由等腰直角三角形的性质可求![]() 的长度.
的长度.
证明:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
(2)①∵![]() 是直径,
是直径,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,且,
,且,![]()
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 为等腰直角三角形;
为等腰直角三角形;
②∵四边形![]() 是
是![]() 的圆内接四边形,
的圆内接四边形,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)