题目内容
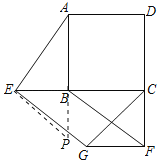
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作FG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
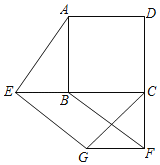
【答案】(1)见解析;(2)见解析;
【解析】
(1)由SAS证明△ABE≌△BCF得出AE=BF,∠BAE=∠CBF,由平行线的性质得出∠CBF=∠CEG,证出AE⊥EG,即可得出结论;
(2)延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,证明△APE≌△ECG得出AE=EG,证出EG=BF,即可得出结论.
证明:(1)![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,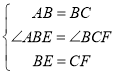 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,如图所示:
,如图所示:
则![]() ,
,![]() ,
,
![]() ,
,
![]() 为正方形
为正方形![]() 外角的平分线,
外角的平分线,
![]() ,
,
![]() ,
,
由(1)得![]() ,
,
在![]() 和
和![]() 中,
中,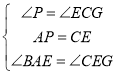 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目