Question

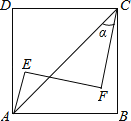
【题目】如图，正方形ABCD内有两点E、F满足AE=4，tanα=，AE⊥EF，CF⊥EF，EF=CF，则正方形的边长为 ．

Answer 1

【答案】10．

【解析】

试题分析：由AE⊥EF，CF⊥EF，AE=4，tanα=，可找出ME的长度以及用CF表示出FM的长度，再由EF=CF，可找出CF的长，结合勾股定理与正方形的性质即可得出正方形的边长．

解：令EF与AC的交点为点M，如图所示．

∵AE⊥EF，CF⊥EF，

∴∠AEM=∠CFM=90°，

∵∠AME=∠CMF，

∴△AME∽CMF，

∴∠EAM=∠FCM=α．

∵AE=4，tanα=，

∴EM=3，FM=CF，

∵EF=EM+FM=3+CF=CF，

∴CF=12，FM=9．

由勾股定理可知：AM==5，CM==15，

∴AC=AM+CM=20．

∵四边形ABCD为正方形，

∴AB=AC=10．