题目内容
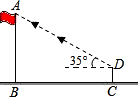 在课外活动中,一个小组测量学校旗杆的高度,如图,他们在距离旗杆底部B点8米的C点处竖立一根高为1.6米的标杆CD,当从标杆顶部D看旗杆顶部A点时,仰角刚好是35°,那么旗杆AB的高度(精确到0.1米)大约是
在课外活动中,一个小组测量学校旗杆的高度,如图,他们在距离旗杆底部B点8米的C点处竖立一根高为1.6米的标杆CD,当从标杆顶部D看旗杆顶部A点时,仰角刚好是35°,那么旗杆AB的高度(精确到0.1米)大约是
(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
- A.6.6
- B.6.8
- C.7
- D.7.2
D
分析:过D作AB的垂线,在构造的直角三角形中,利用BC的长和已知的角的度数,利用正切函数可求得AB的长.
解答: 解:过点D作DF⊥AB于F.
解:过点D作DF⊥AB于F.
由题意则DF=BC,即DF=8米.
在直角△ADF中,∠ADF=35°,
AF=DFtan35°=8×0.7002=5.6016(米).
则AB=AF+FB=5.6016+1.6≈7.2(米).
故选D.
点评:本题主要利用了直角三角形的边角关系来解题,通过构造直角三角形,将实际问题转化为数学问题是解答此类题目的关键所在.
分析:过D作AB的垂线,在构造的直角三角形中,利用BC的长和已知的角的度数,利用正切函数可求得AB的长.
解答:
 解:过点D作DF⊥AB于F.
解:过点D作DF⊥AB于F.由题意则DF=BC,即DF=8米.
在直角△ADF中,∠ADF=35°,
AF=DFtan35°=8×0.7002=5.6016(米).
则AB=AF+FB=5.6016+1.6≈7.2(米).
故选D.
点评:本题主要利用了直角三角形的边角关系来解题,通过构造直角三角形,将实际问题转化为数学问题是解答此类题目的关键所在.

练习册系列答案
相关题目
 在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?
在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?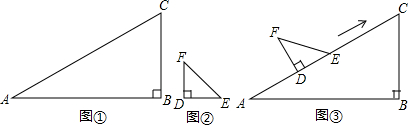
 在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?
在课外活动中,小明发明了一个在直角三角形中画锐角的平分线的方法,他的方法是:如图所示,在斜边AB上取一点E,使BE=BC,过点E作ED⊥AB,交AC于D,那么BD就是∠ABC的平分线,你认为对吗?为什么?