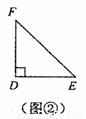题目内容
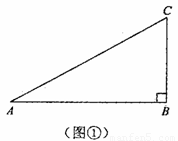
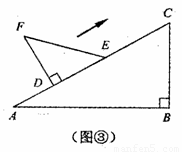
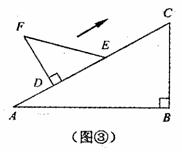
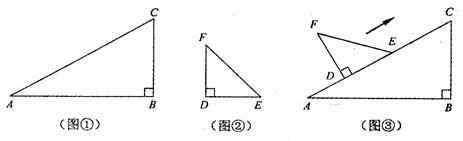
刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠B=90°,∠A=30°,BC=6cm;图②中,∠D=90°,∠E=45°,DE=4cm.图③是刘卫同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).(1)在△DEF沿AC方向移动的过程中,刘卫同学发现:F、C两点间的距离逐渐
(2)刘卫同学经过进一步地研究,编制了如下问题:
问题①:当△DEF移动至什么位置,即AD的长为多少时,F、C的连线与AB平行?
问题②:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
问题③:在△DEF的移动过程中,是否存在某个位置,使得∠FCD=15°?如果存在,求出AD的长度;如果不存在,请说明理由.
请你分别完成上述三个问题的解答过程.
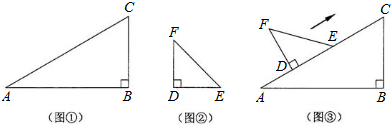
分析:(1)根据题意,观察图形,F、C两点间的距离逐渐变小;
(2)①因为∠B=90°,∠A=30°,BC=6cm,所以AC=12cm,又因为∠FDE=90°,∠DEF=45°,DE=4cm,所以DF=4cm,连接FC,设FC∥AB,则可求证∠FCD=∠A=30°,故AD的长可求;
②设AD=x,则FC2=DC2+FD2=(12-x)2+16,再分情况讨论:FC为斜边;AD为斜边;BC为斜边.综合分析即可求得AD的长;
③假设∠FCD=15°,因为∠EFC=30°,作∠EFC的平分线,交AC于点P,则∠EFP=∠CFP=∠DFE+∠EFP=60°,所以PD=4
cm,PC=PF=2FD=8cm,故不存在.
(2)①因为∠B=90°,∠A=30°,BC=6cm,所以AC=12cm,又因为∠FDE=90°,∠DEF=45°,DE=4cm,所以DF=4cm,连接FC,设FC∥AB,则可求证∠FCD=∠A=30°,故AD的长可求;
②设AD=x,则FC2=DC2+FD2=(12-x)2+16,再分情况讨论:FC为斜边;AD为斜边;BC为斜边.综合分析即可求得AD的长;
③假设∠FCD=15°,因为∠EFC=30°,作∠EFC的平分线,交AC于点P,则∠EFP=∠CFP=∠DFE+∠EFP=60°,所以PD=4
| 3 |
解答: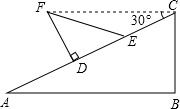 解:(1)变小;
解:(1)变小;
(2)问题①:∵∠B=90°,∠A=30°,BC=6cm
∴AC=12cm
∵∠FDE=90°,∠DEF=45°,DE=4cm
∴DF=4cm
连接FC,设FC∥AB
∴∠FCD=∠A=30°
∴在Rt△FDC中,DC=4
cm
∴AD=AC-DC=(12-4
)cm
∴AD=(12-4
)cm时,FC∥AB;
问题②:设AD=x,在Rt△FDC中,FC2=DC2+FD2=(12-x)2+16
∵AC=12cm,DE=4cm,
∴AD≤8cm,
(I)当FC为斜边时,
由AD2+BC2=FC2得,x2+62=(12-x)2+16,x=
;
(II)当AD为斜边时,
由FC2+BC2=AD2得,(12-x)2+16+62=x2,x=
>8(不合题意舍去);
(III)当BC为斜边时,
由AD2+FC2=BC2得,x2+(12-x)2+16=36,x2-12x+62=0,
方程无解,
∴由(I)、(II)、(III)得,当x=
cm时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形;
另解:BC不能为斜边,
∵FC>CD,∴FC+AD>12
∴FC、AD中至少有一条线段的长度大于6,
∴BC不能为斜边,
∴由(I)、(II)、(III)得,当x=
cm时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形;
问题③:解法一:不存在这样的位置,使得∠FCD=15°
理由如下: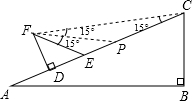
假设∠FCD=15°
∵∠EFC=30°
作∠EFC的平分线,交AC于点P
则∠EFP=∠CFP=15°,∠DFE+∠EFP=60°
∴PD=4
cm,PC=PF=2FD=8cm,
∴PC+PD=8+4
>12
∴不存在这样的位置,使得∠FCD=15°
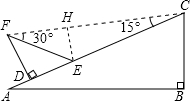
解法二:不存在这样的位置,使得∠FCD=15°
假设∠FCE=15°AD=x
由∠FED=45°
得∠EFC=30°
作EH⊥FC,垂足为H.
∴HE=
EF=2
cm
CE=AC-AD-DE=(8-x)cm
且FC2=(12-x)2+16
∵∠FDC=∠EHC=90°
∠DCF为公共角
∴△CHE∽△CDF
∴
=
又(
)2=(
)2=
∴(
)2=
,即
=
整理后,得到方程x2-8x-32=0
∴x1=4-4
<0(不符合题意,舍去)
x2=4+4
>8(不符合题意,舍去)
∴不存在这样的位置,使得∠FCD=15°.
 解:(1)变小;
解:(1)变小;(2)问题①:∵∠B=90°,∠A=30°,BC=6cm
∴AC=12cm
∵∠FDE=90°,∠DEF=45°,DE=4cm
∴DF=4cm
连接FC,设FC∥AB
∴∠FCD=∠A=30°
∴在Rt△FDC中,DC=4
| 3 |
∴AD=AC-DC=(12-4
| 3 |
∴AD=(12-4
| 3 |
问题②:设AD=x,在Rt△FDC中,FC2=DC2+FD2=(12-x)2+16
∵AC=12cm,DE=4cm,
∴AD≤8cm,
(I)当FC为斜边时,
由AD2+BC2=FC2得,x2+62=(12-x)2+16,x=
| 31 |
| 6 |
(II)当AD为斜边时,
由FC2+BC2=AD2得,(12-x)2+16+62=x2,x=
| 49 |
| 6 |
(III)当BC为斜边时,
由AD2+FC2=BC2得,x2+(12-x)2+16=36,x2-12x+62=0,
方程无解,
∴由(I)、(II)、(III)得,当x=
| 31 |
| 6 |
另解:BC不能为斜边,
∵FC>CD,∴FC+AD>12
∴FC、AD中至少有一条线段的长度大于6,
∴BC不能为斜边,
∴由(I)、(II)、(III)得,当x=
| 31 |
| 6 |
问题③:解法一:不存在这样的位置,使得∠FCD=15°
理由如下:

假设∠FCD=15°
∵∠EFC=30°
作∠EFC的平分线,交AC于点P
则∠EFP=∠CFP=15°,∠DFE+∠EFP=60°
∴PD=4
| 3 |
∴PC+PD=8+4
| 3 |
∴不存在这样的位置,使得∠FCD=15°
解法二:不存在这样的位置,使得∠FCD=15°
假设∠FCE=15°AD=x
由∠FED=45°
得∠EFC=30°
作EH⊥FC,垂足为H.
∴HE=
| 1 |
| 2 |
| 2 |
CE=AC-AD-DE=(8-x)cm
且FC2=(12-x)2+16
∵∠FDC=∠EHC=90°
∠DCF为公共角
∴△CHE∽△CDF
∴
| EC |
| FC |
| HE |
| DF |
| HE |
| DF |
2
| ||
| 4 |
| 1 |
| 2 |

∴(
| EC |
| FC |
| 1 |
| 2 |
| (8-x)2 |
| (12-x)2+16 |
| 1 |
| 2 |
∴x1=4-4
| 3 |
x2=4+4
| 3 |
∴不存在这样的位置,使得∠FCD=15°.
点评:本题把相似三角形的判定和勾股定理结合求解.综合性强,难度大.考查学生综合运用数学知识的能力.注意解题的方法不惟一,可让学生采用不同方法求解,培养学生的思维能力.

练习册系列答案
相关题目
 ,
,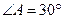 ,
,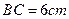 ;图②中,
;图②中,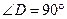 ,
,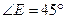 ,
,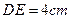 .图③是刘卫同学所做的一个实验:他将
.图③是刘卫同学所做的一个实验:他将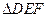 的直角边
的直角边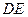 与
与 的斜边
的斜边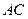 重合在一起,并将
重合在一起,并将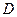 、
、 两点始终在
两点始终在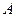 重合).
重合).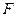 、
、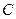 两点间的距离逐渐 ▲ .
两点间的距离逐渐 ▲ .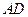 的长为多少时,
的长为多少时,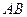 平行?
平行?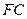 、
、 的长度为三边长的三角形是直角三角形?
的长度为三边长的三角形是直角三角形?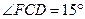 ?如果存在,
?如果存在,
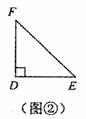
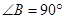 ,
,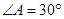 ,
, ;图②中,
;图②中,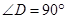 ,
,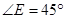 ,
,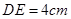 .图③是刘卫同学所做的一个实验:他将
.图③是刘卫同学所做的一个实验:他将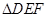 的直角边
的直角边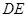 与
与 的斜边
的斜边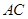 重合在一起,并将
重合在一起,并将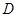 、
、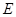 两点始终在
两点始终在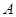 重合).
重合).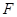 、
、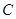 两点间的距离逐渐 ▲ .
两点间的距离逐渐 ▲ .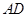 的长为多少时,
的长为多少时,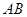 平行?
平行?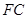 、
、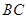 的长度为三边长的三角形是直角三角形?
的长度为三边长的三角形是直角三角形?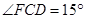 ?如果存在,
?如果存在,