Question

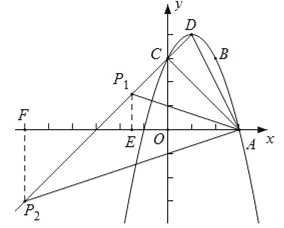
【题目】如图，已知在平面直角坐标系xOy中，二次函数y=﹣x2+mx+n的图象经过点A（3，0），B（m，m+1），且与y轴相交于点C．

（1）求这个二次函数的解析式并写出其图象顶点D的坐标；

（2）求∠CAD的正弦值；

（3）设点P在线段DC的延长线上，且∠PAO=∠CAD，求点P的坐标．

Answer 1

【答案】（1）y=﹣x2+2x+3，顶点D（1，4）；（2）；（3）（，），（﹣6，﹣3）．

【解析】

试题分析：（1）根据二次函数y=﹣x2+mx+n的图象经过点A（3，0），B（m，m+1），求得m和n的值即可；

（2）根据A，C，D三点的坐标，求得CD=，AC=，AD=，得到CD2+AC2=AD2，根据勾股定理的逆定理得出△ACD是直角三角形，且∠ACD=90°，据此求得∠CAD的正弦值；

（3）先求得直线CD为y=x+3，再设点P的坐标为（a，a+3），然后分两种情况进行讨论：当点P在x轴上方时，过点P作PE⊥x轴于E；当点P在x轴下方时，过点P作PF⊥x轴于F，分别判定△ACD∽△AEP，△ACD∽△AFP，列出比例式求得a的值即可．

试题解析：（1）∵二次函数y=﹣x2+mx+n的图象经过点A（3，0），B（m，m+1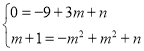），∴，解得：，∴二次函数的解析式为：y=﹣x2+2x+3，顶点D的坐标为（1，4）；

（2）如图所示，在y=﹣x2+2x+3中，当x=0时，y=3，∴C（0，3）．

∵A（3，0），D（1，4），∴CD=，AC=，AD=，∴CD2+AC2=AD2，∴△ACD是直角三角形，且∠ACD=90°，∴sin∠ACD==；

（3）∵直线CD经过C（0，3），D（1，4），∴设可设直线CD为y=kx+b，则

，解得：，∴直线CD为y=x+3，设点P的坐标为（a，a+3），①如图所示，当点P在x轴上方时，过点P作PE⊥x轴于E，则

PE=a+3，AE=3﹣a，∵∠AEP=∠ACD=90°，∠PAO=∠CAD，∴△ACD∽△AEP，∴，即，解得a=，∴a+3=，∴此时P的坐标为（，）；

②如图所示，当点P在x轴下方时，过点P作PF⊥x轴于F，则

PF=﹣（a+3），AF=3﹣a，∵∠AFP=∠ACD=90°，∠PAO=∠CAD，∴△ACD∽△AFP，∴，即，解得a=﹣6，∴a+3=﹣3，∴此时P的坐标为（﹣6，﹣3）；

综上所述，点P的坐标为（，），（﹣6，﹣3）．