题目内容
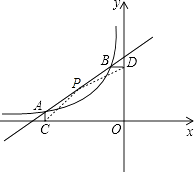
【题目】如图,已知A(﹣4, ![]() ),B(﹣1,2)是一次函数y=kx+b与反比例函数y=
),B(﹣1,2)是一次函数y=kx+b与反比例函数y= ![]() (m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
【答案】
(1)解:由图象得一次函数图象在上的部分,﹣4<x<﹣1,
当﹣4<x<﹣1时,一次函数大于反比例函数的值
(2)解:设一次函数的解析式为y=kx+b,
y=kx+b的图象过点(﹣4, ![]() ),(﹣1,2),则
),(﹣1,2),则
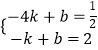 ,
,
解得 ![]()
一次函数的解析式为y= ![]() x+
x+ ![]() ,
,
反比例函数y= ![]() 图象过点(﹣1,2),
图象过点(﹣1,2),
m=﹣1×2=﹣2
(3)解:连接PC、PD,如图,
设P(x, ![]() x+
x+ ![]() )
)
由△PCA和△PDB面积相等得
![]() ×
× ![]() ×(x+4)=
×(x+4)= ![]() ×|﹣1|×(2﹣
×|﹣1|×(2﹣ ![]() x﹣
x﹣ ![]() ),
),
x=﹣ ![]() ,y=
,y= ![]() x+
x+ ![]() =
= ![]() ,
,
∴P点坐标是(﹣ ![]() ,
, ![]() ).
).
【解析】(1)根据一次函数图象在上方的部分是不等式的解,观察图象,可得答案;(2)根据待定系数法,可得函数解析式;(3)根据三角形面积相等,可得答案.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目