题目内容
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF=![]() OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.
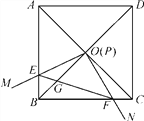
【答案】(1)(2)(3)(5)
【解析】分析:
(1)由四边形ABCD是正方形,直角∠MPN,易证得△BOE≌△COF(ASA),则可证得结论;
(2)由(1)易证得S四边形OEBF=S△BOC=![]()
![]() S正方形ABCD,则可证得结论;
S正方形ABCD,则可证得结论;
(3)由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+BF=![]() OA;
OA;
(4)首先设AE=x,则BE=CF=1﹣x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;
(5)易证得△OEG∽△OBE,然后由相似三角形的对应边成比例,证得OGOB=OE2,再利用OB与BD的关系,OE与EF的关系,即可证得结论.
【解答】解:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
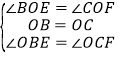 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=![]() OE;故正确;
OE;故正确;
(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
(3)∴BE+BF=BF+CF=BC=![]() OA;故正确;
OA;故正确;
(4)过点O作OH⊥BC,
∵BC=1,
∴OH=![]() BC=
BC=![]() ,
,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x(1﹣x)+
x(1﹣x)+![]() (1﹣x)×
(1﹣x)×![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=![]() 时,S△BEF+S△COF最大;
时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;故错误;
;故错误;
(5)∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OGOB=OE2,
∵OB=![]() BD,OE=
BD,OE=![]() EF,
EF,
∴OGBD=EF2,
∵在△BEF中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
∴OGBD=AE2+CF2.故正确.
故答案为:(1),(2),(3),(5).



【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
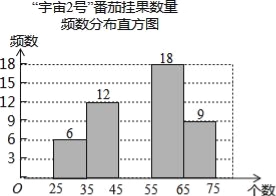
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
【题目】某商场经营一批进价2元一件的小商品,在市场销售中发现此商品日销售单价x(元)与日销售量y(件)之间有如下关系:
x | 3 | 5 | 9 | 11 |
y | 18 | 14 | 6 | 2 |
(1)猜想日销售量y(件)与日销售单价x(元)之间可能存在怎样函数关系式?用你所学知识确定y与x之间的函数关系式,并验证你的猜想。
(2)设经营此商品的日销售利润为P(元),根据日销售规律:
①试求出日销售利润P(元)与日销售单价x之间的关系式,并求出日销售单价x为多少时,才能获得最大日销售利润,最大日销售利润为多少元?
②分别写出x和P的取值范围。