题目内容
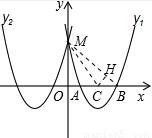
如图,已知抛物线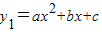 与抛物线
与抛物线 关于y轴对称,并与y轴交于点M,与x轴交于A、B两点.
关于y轴对称,并与y轴交于点M,与x轴交于A、B两点.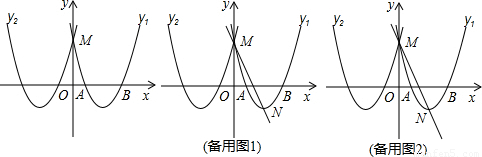
(1)求抛物线y1的解析式;
(2)若AB的中点为C,求sin∠CMB;
(3)若一次函数y=kx+h的图象过点M,且与抛物线y1交于另一点N(m,n),其中m≠n,同时满足m2-m+t=0和n2-n+t=0(t为常数).
①求k值;
②设该直线交x轴于点D,P为坐标平面内一点,若以O、D、P、M为顶点的四边形是平行四边形,试求P点的坐标.(只需直接写出点P的坐标,不要求解答过程)
【答案】分析:(1)对与函数 ,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;
,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;
(2)过点C作CH⊥MB于点H,求出CB、MC,及△CMB的面积,然后利用勾股定理求出MB的长度,继而可得出CH的长度,在RT△MNH中可求出sin∠CMB的值;
(3)先根据题意得出直线y=kx+h中k的可能值,然后分类讨论得出点D的坐标,根据平行四边形的性质即可得出点P的坐标.
解答:解:(1)对于函数 来说,令x=0,则y=5,
来说,令x=0,则y=5,
∴M(0,5),
令y=0,则x2+6x+5=0,
∴x1=-1,x2=-5,
∴抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),
∵抛物线y1、y2关于y轴对称,
∴A(1,0),B(5,0).…(3分)
故可设y1=a(x-1)(x-5),将点M(0,5)代入,得y1=(x-1)(x-5),即 .…(4分)
.…(4分)
(2)∵A(1,0),B(5,0),M(0,5),C为AB的中点,
∴C(3,0),CB=2,MC= ,
,
∴S△CMB= CB•OM=
CB•OM= ×2×5=5,
×2×5=5,
∵OM=OB=5,
∴由勾股定理可得MB=5 ,
,
过点C作CH⊥MB于点H,则 ×5
×5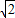 -CH=5,
-CH=5,
∴CH= ,
,
在Rt△MCH中,sin∠CMB= =
=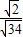 =
= .
.
(3)①∵直线y=kx+h过点M(0,5),
∴h=5,
∵N(m,n)在抛物线y1上,
∴n=m2-6m+5,
又∵m2-m+t=0,n2-n+t=0,
故两式相减,得:m2-n2-m+n=0,即(m-n)(m+n-1)=0.
∵m≠n,
∴m+n-1=0,即n=1-m,
将n=1-m代入n=m2-6m+5得:m2-5m+4=0,
∴m1=1,m2=4.从而n1=0,n2=-3,
∴N1(1,0),N2(4,-3),
故将它们的坐标分别代入y=kx+5中,得k1=-5,k2=-2.
②当k=-5时,直线为y=-5x+5,此时D,N与A点重合.
因此满足条件的P点有三个:P1(1,5),P2(-1,5),P3(1,-5).
当k=-2时,直线为y=-2x+5,此时D( ,0).
,0).
因此满足条件的P点也有三个:P4( ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5).
综上,满足条件的P点共有六个:P1(1,5),P2(-1,5),P3(1,-5),P4( ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5).
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点,主要考查学生数形结合的数学思想方法.
 ,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;
,令x=0,可得y=5,从而可得出点M的坐标,令y=0,可求出x1=-1,x2=-5,从而得出抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),结合轴对称的知识,可设y1=a(x-1)(x-5),将点M(0,5)代入,即可得出解析式;(2)过点C作CH⊥MB于点H,求出CB、MC,及△CMB的面积,然后利用勾股定理求出MB的长度,继而可得出CH的长度,在RT△MNH中可求出sin∠CMB的值;
(3)先根据题意得出直线y=kx+h中k的可能值,然后分类讨论得出点D的坐标,根据平行四边形的性质即可得出点P的坐标.
解答:解:(1)对于函数
 来说,令x=0,则y=5,
来说,令x=0,则y=5,∴M(0,5),
令y=0,则x2+6x+5=0,
∴x1=-1,x2=-5,
∴抛物线y2与x轴两交点的坐标为(-1,0),(-5,0),
∵抛物线y1、y2关于y轴对称,
∴A(1,0),B(5,0).…(3分)
故可设y1=a(x-1)(x-5),将点M(0,5)代入,得y1=(x-1)(x-5),即
 .…(4分)
.…(4分)(2)∵A(1,0),B(5,0),M(0,5),C为AB的中点,
∴C(3,0),CB=2,MC=
 ,
,∴S△CMB=
 CB•OM=
CB•OM= ×2×5=5,
×2×5=5,∵OM=OB=5,
∴由勾股定理可得MB=5
 ,
,过点C作CH⊥MB于点H,则
 ×5
×5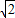 -CH=5,
-CH=5,
∴CH=
 ,
,在Rt△MCH中,sin∠CMB=
 =
=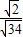 =
= .
.(3)①∵直线y=kx+h过点M(0,5),
∴h=5,
∵N(m,n)在抛物线y1上,
∴n=m2-6m+5,
又∵m2-m+t=0,n2-n+t=0,
故两式相减,得:m2-n2-m+n=0,即(m-n)(m+n-1)=0.
∵m≠n,
∴m+n-1=0,即n=1-m,
将n=1-m代入n=m2-6m+5得:m2-5m+4=0,
∴m1=1,m2=4.从而n1=0,n2=-3,
∴N1(1,0),N2(4,-3),
故将它们的坐标分别代入y=kx+5中,得k1=-5,k2=-2.
②当k=-5时,直线为y=-5x+5,此时D,N与A点重合.
因此满足条件的P点有三个:P1(1,5),P2(-1,5),P3(1,-5).
当k=-2时,直线为y=-2x+5,此时D(
 ,0).
,0).因此满足条件的P点也有三个:P4(
 ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5).综上,满足条件的P点共有六个:P1(1,5),P2(-1,5),P3(1,-5),P4(
 ,5),P5(-
,5),P5(- ,5),P6(
,5),P6( ,-5).
,-5).点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点,主要考查学生数形结合的数学思想方法.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
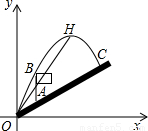
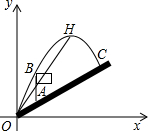 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 米,旗杆AB高为3米,C点的垂
米,旗杆AB高为3米,C点的垂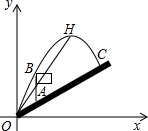 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.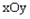 中,抛物线
中,抛物线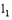 的解析式为
的解析式为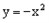 ,将抛物线
,将抛物线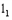 平移后得到抛线物
平移后得到抛线物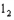 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。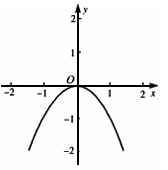
 (1)求这个抛物线的解析式;
(1)求这个抛物线的解析式; 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.