��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=ax2+2xa+c����A����4��0����B��0��4�����㣬��x�ύ����һ��C��ֱ��y=x+5��x�ύ�ڵ�D����y�ύ�ڵ�E��
��1���������ߵĽ���ʽ��
��2����P�ǵڶ������������ϵ�һ�����㣬����EP������E��EP�Ĵ���l����l�Ͻ�ȡ�߶�EF��ʹEF=EP���ҵ�F�ڵ�һ���ޣ�����F��FM��x���ڵ�M�����P�ĺ�����Ϊt���߶�FM�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
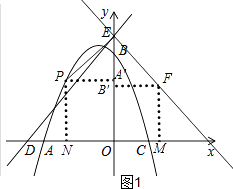
��3���ڣ�2���������£�����E��EH��ED��MF���ӳ����ڵ�H������DH����GΪDH���е㣬��ֱ��PG����AC���е�Qʱ�����F�����꣮
���𰸡�
��1��
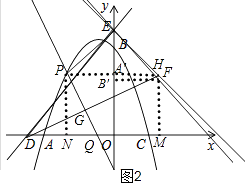
�⣺��A����4��0����B��0��4������y=ax2+2xa+c�� ![]() �����
����� 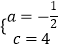 ��
��
���������߽���ʽΪy=�� ![]() x2��x+4��
x2��x+4��
��2��
�⣺��ͼ1��
�ֱ��P��F��y�������ߣ�����ֱ�ΪA�䡢B�䣬��P��PN��x�ᣬ����ΪN��
��ֱ��DE�Ľ���ʽΪ��y=x+5����E��0��5����
��OE=5��
�ߡ�PEO+��OEF=90�㣬��PEO+��EPA��=90�㣬
���EPA��=��OEF��
��PE=EF����EA��P=��EB��F=90�㣬
���PEA��ա�EFB�䣬
��PA��=EB��=��t��
��d=FM=OB��=OE��EB��=5������t��=5+��
��3��
�⣺��ͼ2��
��ֱ��DE�Ľ���ʽΪ��y=x+5��
��EH��ED��
��ֱ��EH�Ľ���ʽΪ��y=��x+5��
��FB��=A��E=5������ ![]() t2��t+4��=
t2��t+4��= ![]() t2+t+1��
t2+t+1��
��F�� ![]() t2+t+1��5+t����
t2+t+1��5+t����
���H�ĺ�����Ϊ�� ![]() t2+t+1��
t2+t+1��
y=�� ![]() t2��t��1+5=��
t2��t��1+5=�� ![]() t2��t+4��
t2��t+4��
��H�� ![]() t2+t+1����
t2+t+1���� ![]() t2��t+4����
t2��t+4����
��G��DH���е㣬
��G�� ![]() ��
�� ![]() ����
����
��G�� ![]() t2+
t2+ ![]() t��2����
t��2���� ![]() t2��
t2�� ![]() t+2����
t+2����
��PH��x�ᣬ
��DG=GH��
��PG=GQ��
�� ![]() =
= ![]() t2+
t2+ ![]() t��2��
t��2��
t= ![]()
![]() ��
��
��P�ڵڶ����ޣ�
��t��0��
��t=�� ![]() ��
��
��F��4�� ![]() ��5��
��5�� ![]() ����
����
�������������Ƕ��κ������ۺ��⣬���������ô���ϵ��������κ�����һ�κ����Ľ���ʽ��������ֱ��������ȫ�ȵ����ʺ��ж�������Ĺؼ��Ǹ���ֱ��������ȫ�ȶ�Ӧ�������ʽ�ó�d��t�ĺ�����ϵʽ��ͬʱҪע�⣺��A��B���������ֱ�Ϊ��x1��y1������x2��y2�������߶�AB�е������Ϊ�� ![]() ��
�� ![]() ������1�����ô���ϵ��������κ����Ľ���ʽ����2����ͼ1���������߹�������ֱ�������Σ�����б��PE=EF���������֤��ֱ��������ȫ�ȣ���PA��=EB�䣬��d=FM=OE��EB�������ʽ�ɵý��ۣ���Ҫע��PA��=��t����3����ͼ2������ֱ��EH�Ľ���ʽ��ʾ����F�������H�����꣬���ֵ�P�͵�H����������ȣ���PH��x��ƽ�У�����ƽ���߽��߶γɱ��������ɵ�GҲ��PQ���е㣬�ɴ˱�ʾ����G�����겢��ʽ�����t��ֵ��ȡ�ᣬ�������F�����꣮
������1�����ô���ϵ��������κ����Ľ���ʽ����2����ͼ1���������߹�������ֱ�������Σ�����б��PE=EF���������֤��ֱ��������ȫ�ȣ���PA��=EB�䣬��d=FM=OE��EB�������ʽ�ɵý��ۣ���Ҫע��PA��=��t����3����ͼ2������ֱ��EH�Ľ���ʽ��ʾ����F�������H�����꣬���ֵ�P�͵�H����������ȣ���PH��x��ƽ�У�����ƽ���߽��߶γɱ��������ɵ�GҲ��PQ���е㣬�ɴ˱�ʾ����G�����겢��ʽ�����t��ֵ��ȡ�ᣬ�������F�����꣮
�����㾫��������ȷ��һ�κ����ı���ʽ�ǽ����ĸ�������Ҫ֪��ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�����Ŀ��Ϊ������У������������ɫѧУ��ij�ؽ�����ί���ֹ�˾��A��B��У����У�̻�����֪AУ����ͼ![]() ����Ӱ���ֿյ��������ƺ��BУ����ͼ
����Ӱ���ֿյ��������ƺ��BУ����ͼ![]() ����Ӱ���ֿյ��������ƺ���ڼס������طֱ���ͬ�ֲ�Ƥ3500��
����Ӱ���ֿյ��������ƺ���ڼס������طֱ���ͬ�ֲ�Ƥ3500��![]() ��2500��
��2500��![]() ���ۣ����ۼ�һ�������ֹ�˾��ס������ع����Ƥ����·�̺��˷ѵ��۱����£�
���ۣ����ۼ�һ�������ֹ�˾��ס������ع����Ƥ����·�̺��˷ѵ��۱����£�
·�̡��˷ѵ��۱�
AУ | BУ | |||
·�� | �˷ѵ��� | ·�� | �˷ѵ��� | |
�� | 20 |
| 10 |
|
�ҵ� | 15 |
| 20 | |
![]() ע���˷ѵ��۱�ʾÿƽ���ײ�Ƥ����1ǧ������������
ע���˷ѵ��۱�ʾÿƽ���ײ�Ƥ����1ǧ������������![]()

��![]() �ֱ����ͼ1��ͼ2����Ӱ���������
�ֱ����ͼ1��ͼ2����Ӱ���������
![]() ���ֹ�˾����
���ֹ�˾����![]() �IJ�Ƥȫ������AУ����������ֹ�˾���Ͳ�ƤȥA��B��У�����˷ѣ�
�IJ�Ƥȫ������AУ����������ֹ�˾���Ͳ�ƤȥA��B��У�����˷ѣ�
![]() �������һ�����ͷ�����ʹ���ֹ�˾֧�����Ͳ�Ƥ�����˷Ѳ�����15000Ԫ��
�������һ�����ͷ�����ʹ���ֹ�˾֧�����Ͳ�Ƥ�����˷Ѳ�����15000Ԫ��


