题目内容
【题目】综合与探究
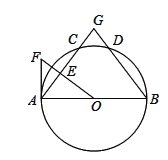
(1)操作发现:如图1,点D是等边△ABC边BA上一动点(点D与点B不重合),连结DC,以DC为边在CD上方作等边△DCF,连结AF,你能发现线段AF与BD之间的数量关系吗?证明你发现的结论.
(2)类比猜想:如图2,当动点D运动至等边△ABC边BA的延长线上时,其余条件不变,猜想:(1)中的结论是否成立,并说明理由.
(3)拓展探究:如图3.当动点D在等边△ABC边BA上运动时(点D与点B不重合),连结DC,以DC为边在CD上方和下方分别作等边△DCF和等边△DCF′,连结AF,BF′,探究:AF、BF′与AB有何数量关系?并说明理由.
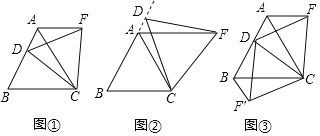
【答案】(1)AF=BD,证明见解析;(2)AF=BD,理由见解析;(3)AF+BF′=AB,理由见解析.
【解析】
(1)如图①中中,结论:AF=BD.证明△BCD≌△ACF(SAS)可得结论.
(2)如图②中,结论:AF=BD.证明△BCD≌△ACF(SAS)可得结论.
(3)如图③中.结论:AF+BF′=AB.利用全等三角形的性质解决问题即可.
解:(1)如图①中中,结论:AF=BD.
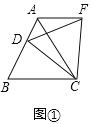
理由:∵△ABC,△DCF都是等边三角形,
∴CB=CA,CD=CF,∠BCA=∠DCF=60°,
∴∠BCD=∠ACF,
∴△BCD≌△ACF(SAS),
∴BD=CF.
(2)如图②中,结论:AF=BD.
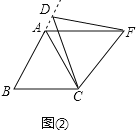
理由:∵△ABC,△DCF都是等边三角形,
∴CB=CA,CD=CF,∠BCA=∠DCF=60°,
∴∠BCD=∠ACF,
∴△BCD≌△ACF(SAS),
∴BD=CF.
(3)如图③中.结论:AF+BF′=AB.

理由:∵△ABC,△DCF都是等边三角形,
∴CB=CA,CD=CF,∠BCA=∠DCF=60°,
∴∠BCD=∠ACF,
∴△BCD≌△ACF(SAS),
∴BD=CF.
同法可证:△ACD≌△BCF′(SAS),
∴AD=BF′,
∴AF+BF′=BD+AD=AB.

【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h) 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离(km) | 5 |
| 20 |
乙与A地的距离(km) | 0 | 12 |
|
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.