题目内容
【题目】列一元一次方程解应用题
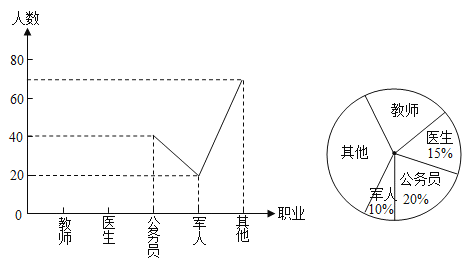
为发展校园足球运动,某区四校决定联合购买![]() 套队服和
套队服和![]() (
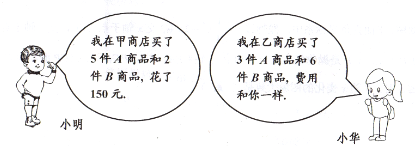
(![]() 且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多
且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多![]() 元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过
元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过![]() 套,则购买足球打八折
套,则购买足球打八折
(1)求每套队服和每个足球的价格是多少?
(2)请用含![]() 的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
(3)求出到甲、乙两家购买所需花的费用相同时![]() 的值.
的值.
【答案】(1)每套队服的价格为150元,每个足球的价格为100元;(2)100a+14000; 80a+15000;(3)到甲、乙两家购买所需花的费用相同时a的值为50
【解析】
(1)设每个足球的价格为x元,则每套队服的价格为(x+50)元,根据两套队服与三个足球的费用相等列方程解答即可得到答案;
(2)甲商场的费用=队服的费用+花钱足球的费用;乙商场的费用=队服的费用+足球费用的八折;
(3)将(2)甲乙两家商场的代数式相等得到方程,解方程即可得到答案.
(1)设每个足球的价格为x元,则每套队服的价格为(x+50)元,
根据题意得:2(x+50)=3x,
解得:x=100,
∴x+50=150.
答:每套队服的价格为150元,每个足球的价格为100元.
(2)到甲商场购买所花的费用为:150×100+100(a﹣![]() )=100a+14000(元),
)=100a+14000(元),
到乙商场购买所花的费用为:150×100+0.8×100a=80a+15000(元).
故答案为:100a+14000,80a+15000.
(3)根据题意得:100a+14000=80a+15000,
解得:a=50.
答:到甲、乙两家购买所需花的费用相同时a的值为50.

【题目】北京地铁1号线(BeijingSubwayLine1),是中国第一条地铁线路,1969年10月1日,第一辆地铁机车从古城站呼啸驶出.北京地铁一期工程赶在新中国成立20周年的时侯建成通车了,宣告了中国没有地铁历史的结束.
下图是北京1号线地铁部分相邻站间距信息统计表.
1号线部分相邻站间距信息统计表 | ||
起始/终到车站 | 区间距离(单位:km) | 近似区间距离(精确到个位) |
玉泉路﹣﹣八宝山 | 1.479 |
|
八宝山﹣﹣八角游乐园 | 1.953 |
|
八角游乐园﹣﹣古城 | 1.921 |
|
古城﹣﹣苹果园 | 2.606 |
|
(1)请你填写上表,并利用近似区间距离,选取适当的参照物,借助数轴,尽可能清晰地描绘出上述5个站点的位置;
(2)有如下四个结论:
①当表示八角游乐园的点所表示的数为0,表示八宝山的点所表示的数为﹣2时,表示古城的点所表示的数为2;
②当表示八角游乐园的点所表示的数为0,表示八宝山的点所表示的数为﹣4时,表示古城的点所表示的数为4;
③当表示八角游乐园的点所表示的数为1,表示八宝山的点所表示的数为﹣3时,表示古城的点所表示的数为5;
④当表示八角游乐园的点所表示的数为﹣1,表示八宝山的点所表示的数为﹣5时,表示古城的点所表示的数为3.
上述结论中,所有正确结论的序号是 .