��Ŀ����
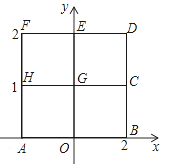
����Ŀ����ͼ��2��2����ÿ��С�����εı߳�Ϊ1��������A��O��B��C��D��E��F��H��G�Ÿ���㣮������l�Ľ���ʽΪy=![]() x2+bx+c��
x2+bx+c��
��1����l������O��0��0����B��1��0������b= ��c= ��������������һ��������Ϊ ��
��2����l������H����1��1����G��0��1���������Ľ���ʽ������������ͨ������˵����D��1��2���Ƿ���l����
��3����l������Ÿ�����е�������ֱ��д���������������������ߵ�������

���𰸡��⣺��1��![]() ��0������1��1������2����D��1��2����������l�ϣ���3��������������������4����
��0������1��1������2����D��1��2����������l�ϣ���3��������������������4����
�������������������1����������������ʽ���ɵõ�����b��c�ķ����飬�Ӷ����b��c��ֵ��Ȼ��Ѹ������������ʽ�����жϣ�
��2���루1���Ľⷨ��ͬ��
��3�����κ����Ķ�����ϵ�����䣬�������ߵ���״�Ϳ��ڷ��䣬���ƶ������ߵĶ��㵽ͼ�е�һ���㣬ͬʱ���������������������߾��Ƿ���Ҫ���ͼ�Σ�
�⣺��1����������ã� 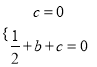 ����ã�
����ã� 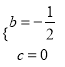 ���ʺ����Ľ���ʽ�ǣ�
���ʺ����Ľ���ʽ�ǣ� ![]() ������H����1��1�����㺯������ʽ������һ�����������ǣ���1��1����
������H����1��1�����㺯������ʽ������һ�����������ǣ���1��1����
�ʴ�Ϊ�� ![]() ��0������1��1����
��0������1��1����
��2����������ã� 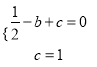 ����ã�
����ã� 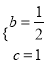 �������Ľ���ʽ�ǣ�
�������Ľ���ʽ�ǣ� ![]() ��
�� ![]() =
=![]() ����������
����������![]() ��
�� ![]() ������D��1��2����������l�ϣ�
������D��1��2����������l�ϣ�
��3����Ϊ��Ŀ�е�a=0.5������������£������ߵĿ��ڷ���Ϳ��ڴ�С��ȷ���ģ�Ӧ����4�����ֱ��HOB���㣬AOC���㣬HGD���㣬����FGC���㣬����������������������������4����