题目内容
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(![]() ,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
(1)直接写出抛物线的解析式 :
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)(0,0),(2,4);(3)存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:
;(2)(0,0),(2,4);(3)存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:![]() 或
或![]() .
.
【解析】
试题(1)先求得B点的坐标,然后根据待定系数法交点抛物线的解析式:
∵A(![]() ,0),对称轴为直线x=1,∴B(4,0).
,0),对称轴为直线x=1,∴B(4,0).
把A(![]() ,0),B(4,0)代入抛物线的表达式得:
,0),B(4,0)代入抛物线的表达式得:
![]() ,解得:
,解得: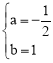 .
.
∴抛物线的解析式为:![]() .
.
(2)根据平移性质及抛物线的对称性,求出A′、C′的坐标.
(3)分AC为平行四边形的边和对角线两种情况讨论即可.
试题解析:解:(1)![]() .
.
(2)∵抛物线的解析式:![]() ,
,
∴当x=0时,y=4. ∴点C(0,4).
∵抛物线的对称轴为x=1,∴点C关于x=1的对称点C′的坐标为(2,4).
∴点C向右平移了2个单位长度.
∴则点A向右平移后的点A′的坐标为(0,0).
∴点A′,C′的坐标分别分(0,0),(2,4).
(3)存在.
设F(x,![]() ).
).
若以A、C、E、F为顶点的四边形为平行四边形,则:
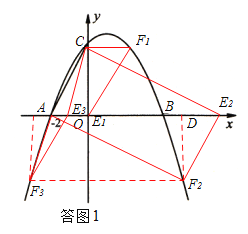
①AC为平行四边形的边,如答图1,
ⅰ)若CFEA为平行四边形,
则CF1∥AE1且CF1=AE1,
此时,E1,F1分别与点A′、C′重合,与题意不符,舍去.
ⅱ)若CEFA为平行四边形,则AC∥FE且AC=FE,
过点F2作F2D⊥x轴于点D,则易证Rt△AOC≌Rt△E2DF2,
∴DE=2,DF2=4.
∴![]() ,解得:
,解得:![]() .
.
∴![]() .
.
∴![]() .
.
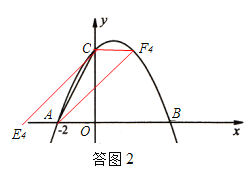
②若AC为平行四边形的对角线,如答图2.
则CF4∥E4A且CF4=E4A,
∴F4(2,4),E4(![]() ,0).
,0).
此时, F4与点C′重合,与题意不符,舍去.
综上所述,存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:![]() 或
或![]() .
.