题目内容
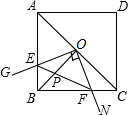 如图,在正方形ABCD中,点O为对角线AC的中点,过点0作射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
如图,在正方形ABCD中,点O为对角线AC的中点,过点0作射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P.则下列结论中:(1)图形中全等的三角形只有两对;
(2)正方形ABCD的面积等于四边形OEBF面积的4倍;
(3)BE+BF=
| 2 |
(4)AE2+CF2=20P•OB.
正确的结论有( )个.
| A、1 | B、2 | C、3 | D、4 |
分析:本题考查正方形的性质,四边相等,四个角都是直角,对角线相等,垂直且互相平分,且平分每一组对角.
解答: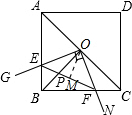 解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
(2)正确.∵△AOE≌△BOF,∴四边形BEOF的面积=△ABO的面积=
正方形ABCD的面积;
(3)正确.BE+BF=AB=
OA;
(4)正确.
AE2+CF2=BE2+BF2=EF2=(
OF)2=2OF2,
在△OPF与△OFB中,
∠OBF=∠OFP=45°,
∠POF=∠FOB,
∴△OPF∽△OFB,
OP:OF=OF:OB,
OF2=OP•OB,
AE2+CF2=20P•OB.
另法:AE2+CF2=BF2+BE2=EF2=(PF+PE)2=PE2+PF2+2PE•PF.
作OM⊥EF,M为垂足.
∵OE=OF,
∴OM=ME=MF.
PE2+PF2=(ME-MP)2+(MF+MP)2=2(MO2+MP2)=2OP2.
∵O、E、B、F四点共圆,
∴PE•PF=OP•PB,
∴AE2+CF2=2OP2+2OP•PB=2OP(OP+PB)=2OP•OB.
故选C.
 解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;
解:(1)错误.△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;(2)正确.∵△AOE≌△BOF,∴四边形BEOF的面积=△ABO的面积=
| 1 |
| 4 |
(3)正确.BE+BF=AB=
| 2 |
(4)正确.
AE2+CF2=BE2+BF2=EF2=(
| 2 |
在△OPF与△OFB中,
∠OBF=∠OFP=45°,
∠POF=∠FOB,
∴△OPF∽△OFB,
OP:OF=OF:OB,
OF2=OP•OB,
AE2+CF2=20P•OB.
另法:AE2+CF2=BF2+BE2=EF2=(PF+PE)2=PE2+PF2+2PE•PF.
作OM⊥EF,M为垂足.
∵OE=OF,
∴OM=ME=MF.
PE2+PF2=(ME-MP)2+(MF+MP)2=2(MO2+MP2)=2OP2.
∵O、E、B、F四点共圆,
∴PE•PF=OP•PB,
∴AE2+CF2=2OP2+2OP•PB=2OP(OP+PB)=2OP•OB.
故选C.
点评:本题考查了正方形的性质,全等三角形的判定和性质,以及勾股定理和相似三角形的判定和性质等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6