题目内容
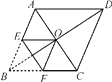
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
【答案】7
【解析】
解:∵四边形ABCD是菱形,AC=2,BD=![]() ,
,
∴∠ABO=∠CBO,AC⊥BD.
∵AO=1,BO=![]() ,
,
∴AB=2,
∴sin∠ABO=![]() =
=![]()
∴∠ABO =30°,
∴∠ABC=∠BAC =60°.
由折叠的性质得,EF⊥BO,BE=EO,BF=FO,∠BEF=∠OEF,;
∵∠ABO=∠CBO,
∴BE=BF,
∴△BEF是等边三角形,
∴∠BEF=60°,
∴∠OEF=60°,
∴∠AEO=60°,
∵∠BAC =60°.
∴△AEO是等边三角形,,
∴AE=OE,
∴BE=AE,同理BF=FC,
∴EF是△ABC的中位线,
∴EF=![]() AC=1,AE=OE=1.
AC=1,AE=OE=1.
同理CF=OF=1,
∴五边形AEFCD的周长为=1+1+1+2+2=7.
故答案为7.

练习册系列答案
相关题目
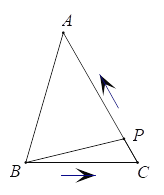
【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.
小新根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y(cm) | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.