题目内容
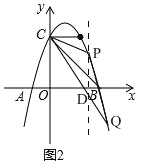
【题目】如图，抛物线y=ax2﹣2ax﹣3a交x轴于点A、B（A左B右），交y轴于点C，S△ABC=6，点P为第一象限内抛物线上的一点．
（1）求抛物线的解析式；
（2）若∠PCB=45°，求点P的坐标；
（3）点Q为第四象限内抛物线上一点，点Q的横坐标比点P的横坐标大1，连接PC、AQ，当PC=
AQ时，求点P的坐标以及△PCQ的面积．
【答案】（1）y=﹣x2+2x+3．（2）P（2，3）；
（3）
.
【解析】
试题分析：（1）利用三角形的面积求出a即可得出抛物线解析式；
（2）先判断出∠OBC=45°，而点P在第一象限，所以得出CP∥OB即：点P和点C的纵坐标一样，即可确定出点P坐标；
（3）根据点P在第一象限，点Q在第二象限，且横坐标相差1，进而设出点P（3﹣m，﹣m2+4m）（0＜m＜1）；得出点Q（4﹣m，﹣m2+6m﹣5），得出CP2，AQ2，最后建立方程求解即可．
试题解析：（1）∵抛物线y=ax2﹣2ax﹣3a=a（x+1）（x﹣3），
∴A（﹣1，0），B（3，0），C（0，﹣3a），
∴AB=4，OC=|﹣3a|=|3a|，
∵S△ABC=6，
∴
ABOC=6，
∴
×4×|3a|=6，
∴a=﹣1或a=1（舍），
∴抛物线的解析式为y=﹣x2+2x+3；
（2）由（1）知，B（3，0），C（0，﹣3a），
∴C（0，3），
∴OB=3，OC=3，
∴△OBC是等腰直角三角形，
∴∠BCO=∠OBC=45°，
∵点P为第一象限内抛物线上的一点，且∠PCB=45°，
∴PC∥OB，
∴P点的纵坐标为3，
由（1）知，抛物线的解析式为y=﹣x2+2x+3，
令y=3，∴﹣x2+2x+3=3，
∴x=0（舍）或x=2，
∴P（2，3）；
（3）如图2，过点P作PD⊥x轴交CQ于D，设P（3﹣m，﹣m2+4m）（0＜m＜1）；
∵C（0，3），
∴PC2=（3﹣m）2+（﹣m2+4m﹣3）2=（m﹣3）2[（m﹣1）2+1]，
∵点Q的横坐标比点P的横坐标大1，
∴Q（4﹣m，﹣m2+6m﹣5），
∵A（﹣1，0）．
∴AQ2=（4﹣m+1）2+（﹣m2+6m﹣5）2=（m﹣5）2[（m﹣1）2+1]
∵PC=
AQ，
∴81PC2=25AQ2，
∴81（m﹣3）2[（m﹣1）2+1]=25（m﹣5）2[（m﹣1）2+1]，
∵0＜m＜1，
∴[（m﹣1）2+1]≠0，
∴81（m﹣3）2=25（m﹣5）2，
∴9（m﹣3）=±5（m﹣5），
∴m=或m=
（舍），
∴P（
，
），Q（
，﹣
），
∵C（0，3），
∴直线CQ的解析式为y=﹣
x+3，
∵P（
，
），
∴D（
，﹣
），
∴PD=
+
=，
∴S△PCQ=S△PCD+S△PQD==PD×xP+=PD×（xQ﹣xP）==PD×xQ==××
=．
