题目内容
在Rt△ABC中,∠BAC=90°,斜边BC上的高AD=4,cosB=0.8,则BC=________.
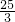
分析:由题意得图:在Rt△ABC中,∠BAC=90°且AD⊥BC,所以得到,△ADB∽△ACB,又已知cosB=0.8,能求出AC,再由cosB=0.8,能求出sinB,根据直角三角形的性质,sinB=
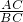 ,则求出BC.
,则求出BC.解答:
 解:已知在Rt△ABC中,∠BAC=90°且AD⊥BC,
解:已知在Rt△ABC中,∠BAC=90°且AD⊥BC,∴△ADB∽△CAB,
∴
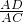 =
=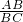 =cosB=0.8,
=cosB=0.8,∴
 =0.8,
=0.8,∴AC=5,
由sin2B+cos2B=1得:sinB=
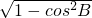 =
= =0.6=
=0.6= ,
,在Rt△ABC中,
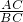 =sinB=
=sinB= ,
,∴
 =
= ,
,∴BC=
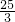 .
.故答案为:
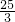 .
.点评:此题考查的知识点是解直角三角形.此题解答的关键是由已知直角三角形和斜边上的高得到相似三角形求出∠B的对边,然后由cosB=0.8求出sinB,进而求出BC.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
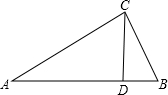 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
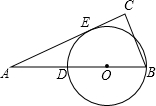 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.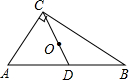 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )