Question

【题目】抛物线经过点和点

求该抛物线所对应的函数解析式；

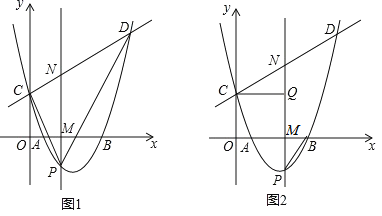
该抛物线与直线相交于两点，点P是抛物线上的动点且位于x轴下方，直线轴，分别与x轴和直线CD交于点M、N．

①连结PC、PD，如图1，在点P运动过程中，的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；

②连结PB，过点C作，垂足为点Q，如图2，是否存在点P，使得与相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．

Answer 1

【答案】 为；(2) ①见解析; ②见解析.

【解析】

(1)由点A、B的坐标，利用待定系数法即可求出b、t的值，结合即可确定b值，此题得解；联立抛物线与直线CD的解析式成方程组，通过解方程组可求出点C、D的坐标，设点P的坐标为，则点N的坐标为，，根据三角形面积公式可得出，利用二次函数的性质即可解决最值问题；利用相似三角形的性质可得出：若与相似，则有或，设点P的坐标为，则点N的坐标为，点M的坐标为，点Q的坐标为，进而可得出，，，，将其代入或中即可求出x的值，结合即可得出点P的坐标．

(1)将、代入，
得：，
解得：，．
，
，
该抛物线所对应的函数解析式为．
联立抛物线与直线CD的解析式成方程组，
得：，
解得：，，
点C的坐标为，点D的坐标为．
设点P的坐标为，则点N的坐标为，
，
．
，
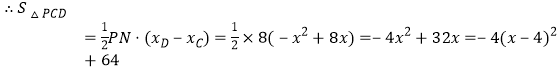当时，取最大值，最大值为64，
在点P运动过程中，的面积存在最大值，最大值为64．

，
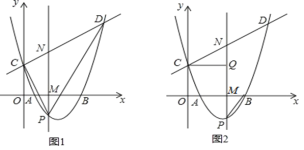
若与相似，则有或．
设点P的坐标为，则点N的坐标为，点M的坐标为，点Q的坐标为，
，，，．
当时，有，
解得：，舍去，
点P的坐标为；
当时，有，
解得：，舍去，
点P的坐标为．
综上所述：存在点P，使得与相似，点P的坐标为或．