题目内容
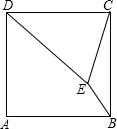
如图,在正方形ABCD中,E是正方形内一点,连接ED、EC、EB,
(1)在图中画出△EDC绕着点C逆时针旋转90°后的三角形,其中E点的对应点为F点(不写作法,保留作图痕迹);
(2)在(1)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
解:(1)如图所示;

(2)连接EF,
设BE=k,CE=2k,
由(1)中可得:CE=CF=2k,∠ECF=90°,
∴EF=2 k,∠CEF=45°,
k,∠CEF=45°,
∵∠BEC=135°,∴∠BEF=90°,
∴BF=3k,
∴在Rt△BEF中,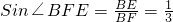 .
.
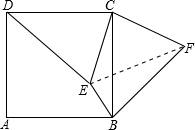
分析:(1)将△EDC顶点D,E绕着点C逆时针旋转90°后,得出答案即可;
(2)利用旋转的性质得出CE=CF,以及EF的长,即可得出sin∠BFE的值.
点评:此题主要考查了图形的旋转以及性质和解直角三角形,根据已知得出用同一未知数表示出CE=CF以及EF的长是解决问题的关键.

(2)连接EF,
设BE=k,CE=2k,
由(1)中可得:CE=CF=2k,∠ECF=90°,
∴EF=2
 k,∠CEF=45°,
k,∠CEF=45°,∵∠BEC=135°,∴∠BEF=90°,
∴BF=3k,
∴在Rt△BEF中,
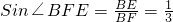 .
.
分析:(1)将△EDC顶点D,E绕着点C逆时针旋转90°后,得出答案即可;
(2)利用旋转的性质得出CE=CF,以及EF的长,即可得出sin∠BFE的值.
点评:此题主要考查了图形的旋转以及性质和解直角三角形,根据已知得出用同一未知数表示出CE=CF以及EF的长是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6