题目内容
某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.
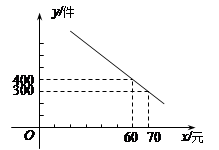
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
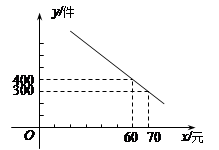
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
(1) y=-10x+1000,50≤x≤70;(2) 70,6000.
试题分析:(1)设y与x的函数关系式为y=kx+b,利用图象经过点(60,400)和(70,300),利用待定系数法求解即可;
(2)用x表示总利润,得到W=-10x2+1500x-50000,根据二次函数最值的求法求当销售单价为70元时,所获得利润有最大值为6000元.
试题解析:(1)最高销售单价为50(1+40%)=70(元),
根据题意,设y与x的函数关系式为y=kx+b(k≠0),
∵函数图象经过点(60,400)和(70,300),
∴
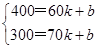 ,
,解得 k=-10,b=1000,
∴y与x之间的函数关系式为y=-10x+1000,
x的取值范围是50≤x≤70;
(2)根据题意,w=(x-50)(-10x+1000),
W=-10x2+1500x-50000,w=-10(x-75)2+6250,
∵a=-10,
∴抛物线开口向下,
又∵对称轴是x=75,自变量x的取值范围是50≤x≤70,
∴w随x的增大而增大,
∴当x=70时,w最大值=-10(70-75)2+6250=6000(元),
∴当销售单价为70元时,所获得利润有最大值为6000元.
考点: 1.二次函数的应用;2.一次函数的应用.

练习册系列答案
相关题目
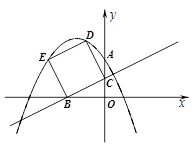
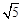 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动. 为对称轴,且在对称轴左侧部分是上升的抛物线的表达式可以是 .
为对称轴,且在对称轴左侧部分是上升的抛物线的表达式可以是 .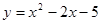 变形为
变形为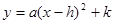 的形式,正确的是( )
的形式,正确的是( )